Deflection
Deflection is similar to bending… but different. Bending concerns us most when it translates into bending failure, which is a bad thing. With deflection, we can tolerate certain amounts of it in certain circumstances. Springiness — or stiffness — in a floor is a characteristic of deflection. Cracking plaster on a ceiling, or separation of taped sheetrock joints, is an indication of excessive deflection.
Deflection is commonly expressed as a percentage or fraction of the span. Two common fractions you will encounter in span tables are V240 and V360 of a span. If a floor sags one inch over 240 inches (20 feet or 6 meters), this is a deflection of V240. A half-inch sag in 180 inches (15 feet or 4.6 meters) is an example of a deflection of V360. Charles Wing, author of several good books on homebuilding and sometimes called the father of the modern owner-builder movement, likes the V360 rule for first floors, where, normally, you don’t want to experience too much springiness.
There are also “rules” for ceilings. If you are supporting a plaster ceiling, deflection should be no greater than V360. With gypsum board, taping, and spackling, you can get by with V240 deflection. For roof rafters, a deflection of V180 is normally allowable by code.
Personally, I don’t use plaster or plasterboard ceilings, and I seldom use any kind of span greater than ten feet, because I put heavy earth roofs on almost every building I’m involved with. So, deflection has never been a big issue. With exposed plank ceilings, V180 of deflection would be fine for roof rafters, and V240 would certainly be acceptable for any floor with a wood ceiling beneath it.
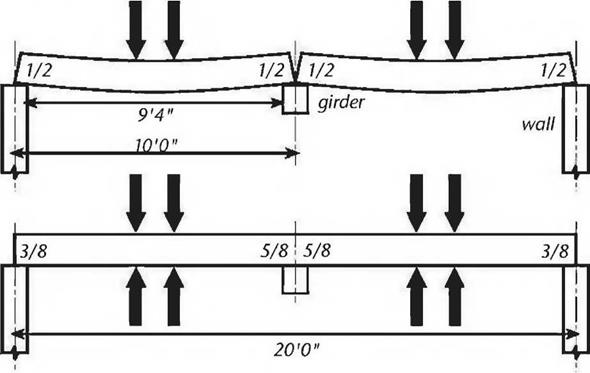
Normally, if a floor joist or roof rafter plan meets the criteria for allowable loads on bending, it will be fine on deflection. Simply use commonly available span tables. I have included examples of some basic span tables in Appendix A, and also a list of where more comprehensive tables can be found. Here is just one example, to give you an idea of the kinds of dimensions we’re talking about, and I get this right out of the new International Residential Code for One – and Two – Family Dwellings, Table R502.3.1(2), a portion of which is reproduced in Appendix A. We assume that this is a residential living area with a live load of 40 pounds per square foot (PSF), a dead load (structural load) of 10 PSF and an allowable deflection of V360. Using Douglas Fir-Larch #1, and with joists 16 inches on center, a two-by-eight can span 13 feet 1 inch (3.99 meters). With two – by-tens, the allowable span increases to 16 feet 5 inches (5.0 meters). With a lesser quality of wood, such as #2 Southern Pine, the allowable spans drop to 12 feet 3 inches (3.12 meters) for two-by-eights and 15 feet 5 inches (4.7 meters) for two-by – tens. For residential sleeping areas, where loads of 30 pounds per square foot is assumed, allowable spans are greater. Find these figures in Appendix A, Table 1, and you will be well on your way to being able to use span tables.
Also in Appendix A, there are two examples of using a rafter span table with a 70-pound snow load and a 20- pound dead load. Back to posts…
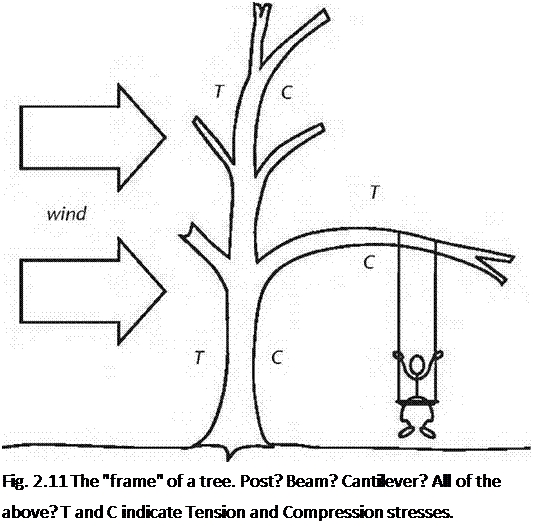 We do not normally think of vertical members, such as posts or even trees, as being beams, but, in fact, they share a lot in common with beams.
We do not normally think of vertical members, such as posts or even trees, as being beams, but, in fact, they share a lot in common with beams.
The word “beam” even comes from an old English word meaning tree or tree trunk. When a tree is being blown by the wind, the windward side is in tension as the tree bends away from the wind. The leeward side is in compression. Actually, as the tree is unsupported at the top, it can be thought of as a cantilever, just another kind of beam. A tree branch, extending out from the trunk, is a cantilever built out from a cantilever. We’ll speak more of cantilevers in a moment.
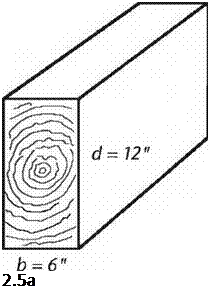
In “post and beam” construction, the posts are the naturally strong component, because they are extremely strong on compression. For example, a six-by-six of a relatively low compressive strength of 1,150 to 1,400 inch-pounds per square inch (you don’t really have to know what this unit means to get the point here; I certainly don’t) will support 32,800 pounds at eight feet of height. That’s 16.4 tons! An eight-by-eight of the same quality will support 63,000 pounds, 31.5 tons.
Tons, I understand. Even with our two stories and heavy earth roof, five of the seven major eight-by-eight posts at Earthwood support about 10,000 pounds each and the other two (full-sized eight-by-eight solid oak) support only 15,000 each, way under their capacity. (An oak eight-by-eight is good for over 93,000 pounds at eight feet of height.) In short, the post part of “post and beam” framing is very strong.
Four-by-fours would actually do for five of the seven posts at Earthwood if it weren’t for our esthetic sensibilities and something called “slenderness ratio” or SR. Visually, a four-by-four supporting an eight-by-eight or ten-by-ten girder just doesn’t look right, like a four-by-eight rafter laid the wrong edge down. But, structurally, the four-by-four post would probably do the job.
“Slenderness ratio” is simply the relationship of the width of the post its length. A 96-inch (8-foot or 2.44-meter high) post that is only four inches wide on its narrowest dimension has an SR of 96 inches/ 4 inches, or 24. Put an eight-by-eight there, and the SR becomes 96 inches/ 8 inches, or 12. The higher the number, the weaker the post. A slender post is much more subject to buckling than compression failure. Lets say we had a four-by-four supporting a heavy load as a post, and that there was a large knot on one or more edges of the post. While knots can be fairly strong in compression, they are weak in tension, as they tend to separate easily from the surrounding wood. A lateral load, such as a sudden impact, or the oscillation during an earthquake, could easily cause such a post to buckle and fail. Extreme vertical loads could do it, as well.






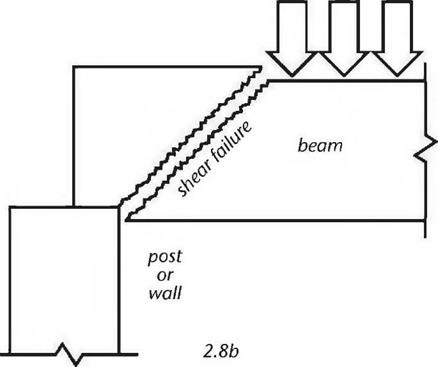
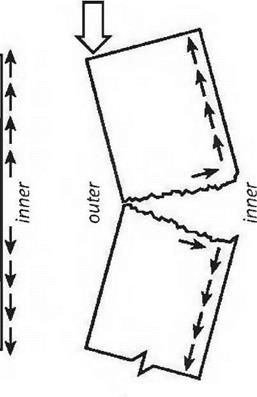
 One good way of explaining shear is to think of it as a combination of compression and tension stresses. Remember that the top surface of a beam is in compression, the bottom surface is in tension, and the centroid (middle part of the beam) is neutral (thus also called the neutral axis.) Fig. 2.8a shows the compression and tension forces at one end of a beam, where it is supported over a post or wall. The arrows show the compression and tension forces. Note that the arrows are pointing in opposite directions, and that the strength of the compression or tension forces diminishes closer to the neutral axis. Fig. 2.8b shows the kind of failure that can happen when the stresses in the beam cause the wood fibers to slide along each other at varying rates. Not surprisingly, the separations often follow annual growth rings. This is why woods prone to shake, such as hemlock, are also low in shear strength. (Shake is the term for a weakness in wood caused by separations between annual growth rings.) It is no coincidence that if a two-by-six hemlock plank is tossed too casually to the ground, it will shatter parallel to the grain.
One good way of explaining shear is to think of it as a combination of compression and tension stresses. Remember that the top surface of a beam is in compression, the bottom surface is in tension, and the centroid (middle part of the beam) is neutral (thus also called the neutral axis.) Fig. 2.8a shows the compression and tension forces at one end of a beam, where it is supported over a post or wall. The arrows show the compression and tension forces. Note that the arrows are pointing in opposite directions, and that the strength of the compression or tension forces diminishes closer to the neutral axis. Fig. 2.8b shows the kind of failure that can happen when the stresses in the beam cause the wood fibers to slide along each other at varying rates. Not surprisingly, the separations often follow annual growth rings. This is why woods prone to shake, such as hemlock, are also low in shear strength. (Shake is the term for a weakness in wood caused by separations between annual growth rings.) It is no coincidence that if a two-by-six hemlock plank is tossed too casually to the ground, it will shatter parallel to the grain.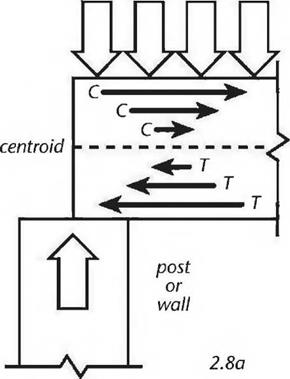




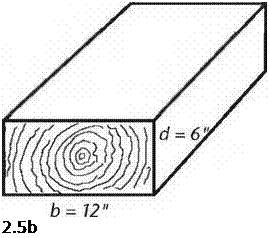 strength of the beam, it will break, usually somewhere in the middle third of the span. This seems logical and natural, just as it seems natural that the two-by-eight plank described above is far more likely to break under a bending load if it is laid flat than if it is installed, properly, on edge. But common sense aside, it is useful to know why this is so from a structural or mathematical standpoint.
strength of the beam, it will break, usually somewhere in the middle third of the span. This seems logical and natural, just as it seems natural that the two-by-eight plank described above is far more likely to break under a bending load if it is laid flat than if it is installed, properly, on edge. But common sense aside, it is useful to know why this is so from a structural or mathematical standpoint.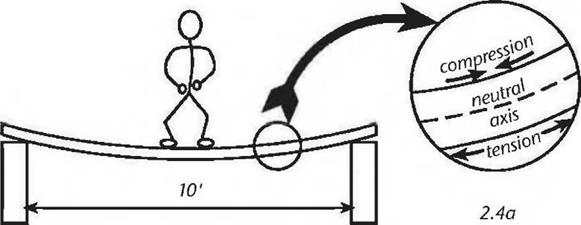
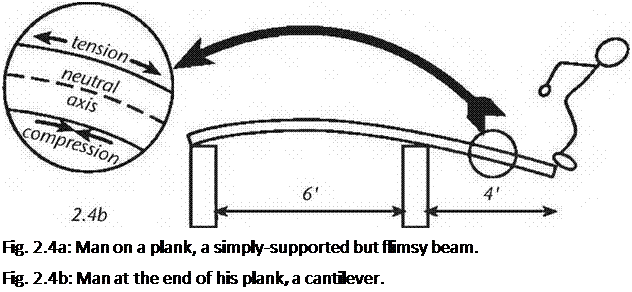 Allowing that this is true — and it is — it follows that an imaginary line along the center of the planks thickness is neither in compression nor tension. This line is known as the centroid or the neutral axis. See Fig. 2.4.
Allowing that this is true — and it is — it follows that an imaginary line along the center of the planks thickness is neither in compression nor tension. This line is known as the centroid or the neutral axis. See Fig. 2.4.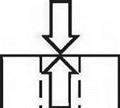
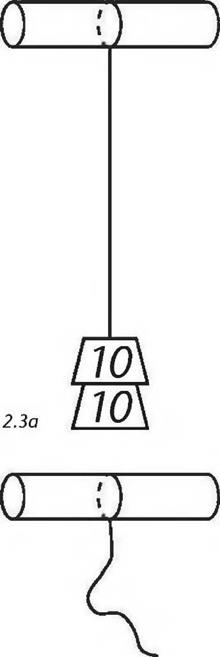

 to stretch the molecules apart. If I hang lead weights on a string, the string is in tension. If I keep adding more lead weights until the tensile strength of the string is exceeded, we will observe a failure in tension: the string breaks.
to stretch the molecules apart. If I hang lead weights on a string, the string is in tension. If I keep adding more lead weights until the tensile strength of the string is exceeded, we will observe a failure in tension: the string breaks. To withstand the loads on it, a house structure must meet three criteria. One, the individual members of the structure, such as beams, joists, and studs, must be strong enough. Two, the members must be attached to one another properly. The joints must be strong. Three, the lumber must be assembled so that the structure as a whole is rigid. (Clark, 1996.)
To withstand the loads on it, a house structure must meet three criteria. One, the individual members of the structure, such as beams, joists, and studs, must be strong enough. Two, the members must be attached to one another properly. The joints must be strong. Three, the lumber must be assembled so that the structure as a whole is rigid. (Clark, 1996.)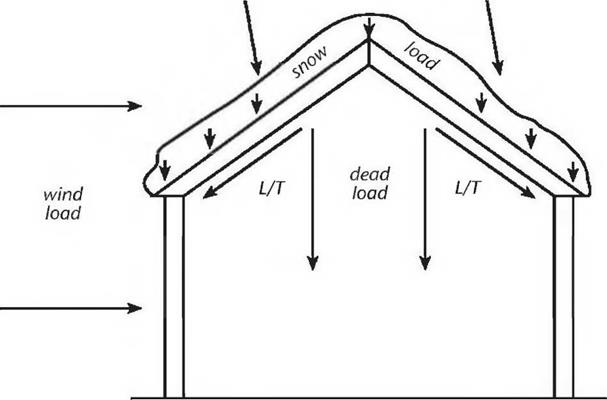 roof is downward, following gravity. But the weakness of such a building is in its joints: the connection between rafters or roof surfaces at the ridge, and the connection of the rafters or roof surface with the posts or sidewalls.
roof is downward, following gravity. But the weakness of such a building is in its joints: the connection between rafters or roof surfaces at the ridge, and the connection of the rafters or roof surface with the posts or sidewalls. Esthetic appeal. Normally, timber frames are left exposed, either on the interior, the exterior, or, in many cases, on both sides of the wall, such as the guesthouses and the garage at Earthwood. With many of the professionally built contemporary timber frame houses, structural insulated panels are fastened to the outside of the frame, and the beautiful heavy timbers are left exposed on the interior, (see Sidebar on page 13) At some 16-sided cordwood homes, the heavy timbers are in evidence on the exterior, but not on the interior. Chapter 6 of my previous book Cordwood Building: The State of the Art [see Bibliography] contains a detailed description of this almost-round timber frame. The method is of most interest to cordwood masonry builders, and is not repeated in this work.
Esthetic appeal. Normally, timber frames are left exposed, either on the interior, the exterior, or, in many cases, on both sides of the wall, such as the guesthouses and the garage at Earthwood. With many of the professionally built contemporary timber frame houses, structural insulated panels are fastened to the outside of the frame, and the beautiful heavy timbers are left exposed on the interior, (see Sidebar on page 13) At some 16-sided cordwood homes, the heavy timbers are in evidence on the exterior, but not on the interior. Chapter 6 of my previous book Cordwood Building: The State of the Art [see Bibliography] contains a detailed description of this almost-round timber frame. The method is of most interest to cordwood masonry builders, and is not repeated in this work.