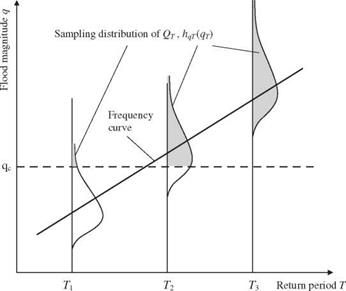
Derivation of Water-Quality Constraints
In a WLA problem, one of the most essential requirements is the assurance of a minimum concentration of dissolved oxygen (DO) throughout the river system in an attempt to maintain desired levels of aquatic biota. The constraint relating the response of DO to the additional of in-stream waste generally is defined by the Streeter-Phelps equation (Eq. 8.60) or its variations (ReVelle et al., 1968; Bathala et al., 1979). To incorporate water-quality constraints into the model formulation, a number of control points are placed within each reach of the river system under investigation. By using the Streeter-Phelps equation, each control point and discharge location becomes a constraint in the LP model, providing a check on water-quality at that location. In a general framework, a typical water quality constraint would be as follows:
Пі Пі
![]() ®ijLj + j < Rt
®ijLj + j < Rt
j=1 j=1
|
|
|
|
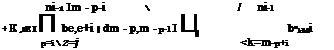 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

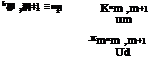 |
|
and
in which M is the total number of control points, Пі is the number of dischargers upstream of the control point i, K“ and Kdd are, respectively, the reareation and deoxygenation coefficients (days-1) in the reach, L0, Q0, and D0 are the upstream waste concentration (mg/L BOD), flow rate (ft3/s), and DO deficit (mg/L), respectively, Ddi, Ldi, and qm are the DO deficit (mg/L), waste concentration (mg/L BOD), and effluent flow rate (ft3/s) from each discharge location, respectively, xdi і is the distance (miles) between discharge location and control point i, and Udi is the average stream velocity (mi/day) in reach ni. Ri represents the allowable DO deficit at the control point i, available for utilization of water discharge (mg/L). It should be noted that in addition to each control point i, water quality is also checked at each discharge location ni.
8.1 
A city in an alluvial valley is subject to flooding. As a matter of good fortune, no serious floods have taken place during the past 50 years, and therefore, no flood – control measure of any significance has been taken. However, last year a serious flood threat developed; people realized the danger they are exposed to, and a flood investigation is under way.
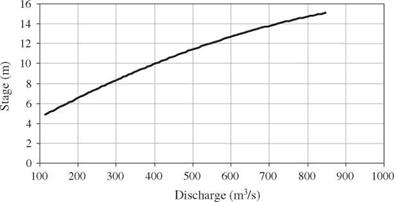
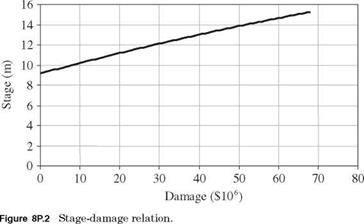
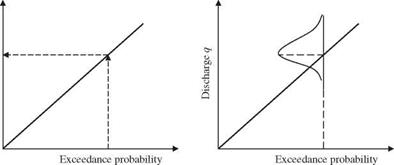
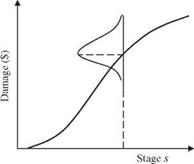
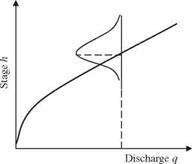
From the hydrologic flood frequency analysis of past streamflow records and hydrometric surveys, the discharge-frequency curve, rating curve, and damage curve under nature condition are derived and shown in the table below and Figs. 8P.1 and 8P.2, respectively. Also, it is known that the flow-carrying capacity of existing channel is 340 m3/s.
T (years) 2 5 10 20 50 100 200 500 1000
Q (m3/s) 255 340 396 453 510 566 623 680 736
Three flood-control alternatives are considered, and they are (1) construction of a dike system throughout the city that will contain a flood peak of 425 m3/s but will fail completely if the river discharge is higher, (2) design of an upstream permanent diversion that would divert up to 85 m3/s if the upstream inflow discharge exceeds existing channel capacity of 340 m3/s, and (3) construction of a detention basin upstream to provide a protection up to a flow of 425 m3/s.
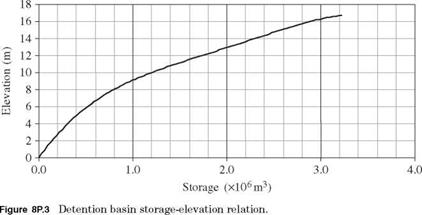
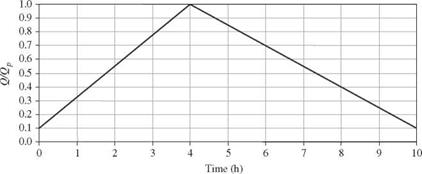
The detention basin will install a conduit with a maximum flow capacity of 340 m3/s. Assume that all flow rates less than 340 m3/s will pass through the conduit without being retarded behind the detention basin. For incoming flow rate between 340 and 425 m3/s, runoff volume will be stored temporally in the detention basin so that outflow discharge does not exceed existing downstream channel capacity. In other words, inflow hydrograph with peak discharge exceeding 425 m3/s could result in spillway overflow, and hence the total outflow discharge would be higher than the channel capacity. The storage-elevation curve at the detention basin site and normalized inflow hydrograph of different return
|
Figure 8P.1 Stage-discharge (rating) curve. |
|
|
periods are shown in Figs. 8P.3 and 8P.4, respectively. The flow capacities of the conduit and spillway can be calculated, respectively, by
Conduit: Qc = 159h05
Spillway: Qs = 67.0(h — hs)15
where Qc and Qs are conduit and spillway capacity (in m3/s), respectively, h is water surface elevation in detention basin (in m) above the river bed, and hs is elevation of spillway crest (in m) above the river bed.
To simplify the algebraic manipulations in the analysis, the basic relations between stage, discharge, storage, and damage are derived to fit the data:
|
|
|
Figure 8P.4 Normalized inflow hydrograph. (Note: Qp = peak inflow discharge.) |
(i) Stage discharge: Q = 8.77 + 7.761 H + 3.1267H2
(ii) Stage damage: D = Max(0, -54.443 + 2.8446H + 0.34035H2)
(iii) Storage elevation: S = 0.0992 + 0.0021h + 0.011h2
h > 0; S = 0, otherwise
in which Q is flow rate in channel (m3/s), H is channel water stage (m), D is flood damage ($106), S is detention basin storage (106 m3), and h is water level in detention basin above channel bed (m).
With all the information provided, answer the following questions:
(a) Develop the damage-frequency curve for the natural condition.
(b) What is the height of spillway crest of the detention basin above the river bed?
(c) Develop the damage-frequency curves as the results of each of the three flood control measures.
(d) Rank the alternatives based on their merits on the flood damage reduction.
8.2 Refer to Problem 8.1 and consider the alternative of building a levee system for flood control. It is known that the capital-cost function for constructing the levee system is
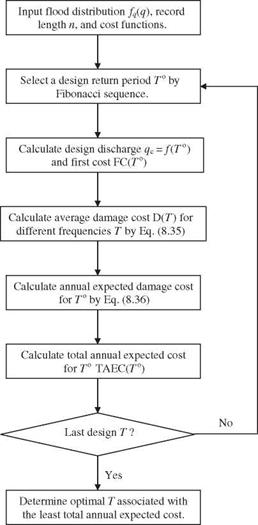
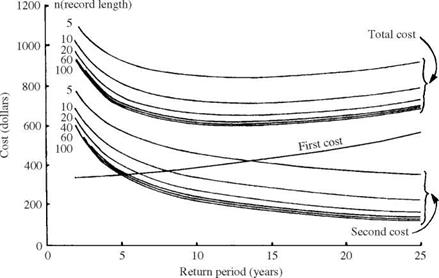
FC(Y) = 1.0 + 0.6(Y – 7) + 0.05(Y – 7)3 in which Y is the height of levee, and FC(Y) is the capital cost (in million dollars). Suppose that the service period of the levee system is to be 50 years and the interest rate is 5 percent. Determine the optimal design return period such that the annual total expected cost is the minimum.
8.3 Consider a confined aquifer with homogeneous soil medium. Use the Thiem equation and the linear superposition principle (see Problem 2.30) to formulate a steady-state optimal groundwater management model for the aquifer system sketched in Fig. 8P.5. The management objective is to determine the maximum total allowable pumpage from the three production wells such that the drawdown of piezometric head at each of the five selected control point would not exceed a specified limit.
+ І
|
@ Production well Control point rik Distance between control point i and well location k
Figure 8P.5 Location of pumping wells and control points for a hypothetical groundwater system (Problems 8.3-8.8). (After Mays and Tung, 1992.) |
(a) Formulate a linear programming model for the groundwater system as shown in Fig. 8P.5.
(b) Suppose that the radius of influence of all pump wells is 700 ft (213 m) and that the aquifer transmissivity is 5000 gal/day/ft (0.00072 m2/s). Based on the information given in Fig. 8P.5, solve the optimization model formulated in part (a).
8.4 Consider that the soil medium is random and that the transmissivity has a lognormal distribution with mean value of 5000 gal/day/ft and a coefficient of variation of 0.4. Construct a chance-constrained model based on Problem 8.3, and solve the chance-constrained model for a 95 percent compliance reliability of all constraints.
8.5 Modify the formulation in Problem 8.3, and solve the optimization model that maximizes the total allowable pumpage in such a way that the largest drawdown among the five control points does not exceed 10 ft.
8.6 Develop a chance-constrained model based on Problem 8.5, and solve the model for a 95 percent compliance reliability of all constraints.
8.7 Based on the chance-constrained model established in Problem 8.6, explore the tradeoff relationship among the maximum total pumpage, compliance reliability, and the largest drawdown.
8.8 Modify the formulation in Problem 8.6 to develop a chance-constrained management model for the hypothetical groundwater system that maximizes the total allowable pumpage while satisfying the desired lowest compliance reliability for all constraints. Furthermore, solve the model for the hypothetical system shown in Fig. 8P.5 with the lowest compliance reliability of 95 percent.
8.9 In the design of a water supply system, it is general to consider a least-cost system configuration that satisfies the required water demand and pressure head at the demand points. The cost of the system may include the initial investment for the components (e. g., pipes, tanks, valves, and pumps) and the operational costs. The optimal design problem, in general, can be cast into
Minimize Capital cost + energy cost subject to (1) Hydraulic constraints
(2) Water demands
(3) Pressure requirements
Consider a hypothetical branched water distribution system as shown in Fig. 8P.6. Develop a linear programming model to determine the optimal combination of cast iron pipe length of various commercially available pipe sizes for each branch. The objective is to minimize the total pipe cost of the system, subject to water demand and pressure constraints at all demand points. The new cast iron pipes of all sizes have the Hazen-Williams roughness coefficient of 130. The cost of pumping head is $500/ft, and the pipe costs for available pipe sizes are listed below
|
Figure 8P.6 A hypothetical water distribution system. |
To this hypothetical system, the required flow rate and water pressure at each demand node are
|
Demand node |
3 |
4 |
5 |
|
Required flow rate (ft3/s) |
6 |
6 |
10 |
|
Minimum pressure (ft) |
550 |
550 |
550 |
[1] Obtain the probability paper corresponding to the distribution one wishes to fit to the data series.
[2] Identify the sample data series to be used. If high-return-period values are of interest, either the annual maximum or exceedance series can be used. If low-return-period values are of interest, use an annual exceedance series.
[3] Rank the data series in decreasing order, and compute exceedance probability or return period using the appropriate plotting-position formula.
[4] Plot the series, and draw a best-fit straight line through the data. An eyeball fit or a mathematical procedure, such as the least-squares method, can be used. Before doing the fit, make a judgment regarding whether or not to include the unusual observations that do not lie near the line (termed outliers).
[5] Compute the sample mean x, standard deviation ax, and skewness coefficient Yx (if needed) for the sample.
[6] Inability to handle distributions with a large skewness coefficient. Table 4.2 indicates that the discrepancy of the failure probability estimated by the MFOSM method for a lognormally distributed performance function becomes larger as the degree of skewness increases. This mainly due to the fact that the MFOSM method incorporates only the first two moments of the random parameters involved. In other words, the MFOSM method simply ignores any moments higher than the second order. Therefore, for those random variables having asymmetric PDFs, the MFOSM method cannot capture such a feature in the reliability computation.
[7] Generally poor estimations of the mean and variance of nonlinear functions. This is evident in that the MFOSM method is the first-order representation
[8] Inappropriateness of the expansion point. In reliability computation, the concern often is those points in the parameter space that fall on the failure surface or limiting-state surface. In the MFOSM method, the expansion point is located at the mean of the stochastic basic variables that do not necessarily define the critical state of the system. The difference in expansion points and the resulting reliability indices between the MFOSM and its alternative, called the advanced first-order, second-moment method (AFOSM), is shown in Fig. 4.3.
[9] The seed X0 can be chosen arbitrarily. If different random number sequences are to be generated, a practical way is to set X0 equal to the date and time when the sequence is to be generated.
2. The modulus m must be large. It may be set conveniently to the word length of the computer because this would enhance computational efficiency. The computation of {aX + c}(mod m) must be done exactly without round-off errors.
3. If modulus m is a power of 2 (for binary computers), select the multiplier a so that a(mod 8) = 5. If m is a power of 10 (for decimal computers), pick a such that a(mod 200) = 21. Selection of the multiplier a in this fashion, along with the choice of increment c described below, would ensure that the random number generator will produce all m distinct possible values in the sequence before repeating itself.
4. The multiplier a should be larger than */m, preferably larger than m/100, but smaller than m -*Jm. The best policy is to take some haphazard constant to be the multiplier satisfying both conditions 3 and 4.
5. The increment parameter c should be an odd number when the modulus m is a power of 2 and c should not be a multiple of 5 when m is a power of 10.
[10] Obtain the eigenvector matrix and diagonal eigenvalue matrix of the correlation matrix Rx or covariance matrix Cx.
[11] Generate K independent standard normal random variates z’ = (z1, z’2
zK У.
[12] Compute the correlated normal random variates X by Eq. (6.36).
[13] Select fx (x) defined over the region of the integral from which n random variates are generated.
[14] Compute g(xi)/fx(xi), for i = 1, 2,…, n.
[15] Calculate the sample average based on Eq. (6.60) as the estimate for G.
[16] Generate K independent standard normal random variates z’ = (z-, z2,…, z’K), and compute the corresponding directional vector e = z’/|z’|
[17] Transform stochastic variables in the original X-space to the independent standard normal Z ‘-space.







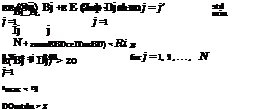

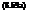 Maximize ^^( Bj + Dj)
Maximize ^^( Bj + Dj)
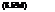 Bj
Bj
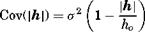 (8.63)
(8.63)
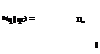 qc < q < qmax (8.39)
qc < q < qmax (8.39)