Appendix В: Stress Load Calculations for Beams
|
S |
pan tables, like the one in Appendix A, will serve for roof design with most structures. With heavy roofs, such as earth roofs, adequate tables are very hard to find. This Appendix shows how to check the girders and rafters in a heavy roof design for shear and bending. Once you have followed through the example, and understand where all the numbers have come from, you should be able to use the formulas and procedures to check other rectilinear designs. Two other books with good information about calculating beam strength are A Timber Framer’s Workshop and Homing Instinct, both listed in Appendix C.
Using this Appendix requires familiarity with basic algebra, specifically the ability to substitute numbers for letters in a formula, and to solve for a single unknown. It is important to keep track of the units (feet, pounds, etc.) as you solve the equations. Please read Chapter 2: Basic Timber Frame Structure, before using this Appendix.
Problem: Test the 40- by 40-foot Log End Cave Plan for the shear and bending strength of the rafters and girders as designed. (The posts and planks are the strong — in some ways overbuilt — components of this design, as discussed in Chapter 2.) A portion of the plan, enough for our purposes, is shown in Fig. A2.1. Girders are labeled “beams” on the plan. The plan is based upon simple 10- foot-square sections, repeated sixteen times, like a chessboard with just four squares on a side. Only six complete sections are shown in the portion reproduced here. Here are the givens:
Earth roof, saturated; 8 inches at io pounds/inch/SF………………………………………………………………………………………. 80 pounds/SF
Crushed stone drainage layer; 2 inches at 10 pounds/inch/SF………………………………………………………………………………………. 20 pounds/SF
Snow load by code, Plattsburgh, NY………………………………………………………………………………………. 70 pounds/SF
Structural load, typical for scale of heavy timber structure
(includes timbers, planking, membrane, and insulation) ……………………………………………………………………………………….. 15 pounds/SF
Total maximum load……………………………………………………………………………………… 185 pounds/SF
Different species of woods have different stress load ratings, and the lumber grade has a large impact on the ratings, too, as can be seen from these few examples from Architectural Graphic Standards:
|
Type of wood |
Grade |
fb1 |
fT |
|
Douglas Fir, Inland Region |
Select Structural |
2,150 |
145 |
|
Douglas Fir, Inland Region |
Common Structural |
1,450 |
95 |
|
Eastern Hemlock |
Select Structural |
1,300 |
85 |
|
Eastern Hemlock |
Common Structural |
1,100 |
60 |
|
Southern Pine |
#1 Dense |
1,700 |
150 |
|
Southern Pine |
#2 |
1,100 |
85 |
1 unit stress for bending in pounds per square inch
2 unit stress for shear in pounds per square inch
For our example, all timbers are assumed to be Douglas Fir (Inland Region, Common Structural) with the following stress load values:
Unit stress for bending (fb) of 1,450 pounds per square inch Unit stress for horizontal shear (fv) of 95 pounds per square inch
These are moderate values, incidentally, similar to Eastern spruce and red and white pine. See Architectural Graphic Standards, The Encyclopedia of Wood, A Timber Framers Workshop and other engineering manuals for stress load ratings for a variety of woods.
Cross-sectional dimensions (b and d): Fig. A2A: A portion of the 40′ x
• Rafters are “five-by-tens,” that is, they are five inches (12.7 cm) in breadth 40′ Log End Cove plan.
(b) and ten inches (25.4 cm) in depth (d).
• Girders (“beams” on the plan) are “eight-by-twelves,” that is, they are eight inches (20.3 cm) in breadth (b) and twelve inches (30.5 cm) in depth (d).
• Rafters are 30 inches o. c., that is: 30 inches (76 cm) is the center-to-center spacing for adjacent members.
• Girders are io feet o. c., that is: ten feet (3 m) is the center-to-center spacing between parallel girders or between girders and the side walls.
• Spans are nominally ten feet (3 m) for both girders and rafters. Actual clear spans, from the edge of one support to the edge of another, is closer to nine feet (2.75 m), but 10 feet is the number used in place of L (span) in the example.
• “Beam” refers to both rafters and girders
• “Simple Span” means that a beam is supported only at its ends. For example, the top half of Fig. 2.10 on page 24 shows two simple-span beams.
• “Double Span” means that a beam is supported at its ends, and also at its midpoint, as in the bottom half of Fig. 2.10.
A = Cross-sectional area (b times d) of beam in square inches b = Breadth of beam, in inches d = Depth of beam, in inches
fb = Allowable unit stress for bending in pounds per square inch fv = Allowable unit stress for shear in pounds per square inch L = Length of span in feet
M = Bending moment in foot-pounds or inch-pounds Mx = Bending moment at the two midspans on a double-span beam
PSF = pounds per square foot
R = Reaction at supports
S = Section modulus of cross-section of beam in inches cubed V = Total shear allowable or actual w = Load or weight per linear foot on beam, in pounds W = Total uniform load or weight on beam, in pounds
/ = The division sign. The value before the division sign is divided by the value after it.
6(8) = 48 or (6)(8) = 48 means “6 times 8 equals 48.” The “times” sign is implied.
bd = A means “b times d equals A.” Again, multiplication is implied.
Formulas used with Simple-Spans:
R = V = wL/z M = wL/8 S = bd2/6 s = M/fb fv = 3V/2A V = wL/z
Formulas used with Double Spans:
Rj = Vj = R3 = V3 = 3WL/8 R2 = 2V2 = iowL/8 V2 = 5WL/8 Mx = 9wL2/i28
We have now listed the five variables for structural design for shear and bending, as discussed in Chapter 2, and we have all the nomenclature and formulas that we need. Now we want to find out if the structure as designed — particularly the rafters and girders — is of adequate strength for both shear and bending to support the design load of 185 pounds per square foot (903 kilos per square meter).
i. Calculating roof load for bending for rafters, simple-span.
(That is, all rafters are about ten feet long, and join over girders.)
S = bd2/6 = (5")(io")2/6 = 83.3 in3 (Section modulus is measured in “inches cubed”)
fb = 1,450 psi (pounds/square inch), given above for Douglas Fir, Inland Region, Common Structural
S = M/fb. By transposition: M = S(fb) = 83.3^(1450 lb/in2) = 120,785 in. lbs
This is the bending moment in “inch-pounds”. To derive the more convenient “foot-pounds,” we need to divide by 12 in/ft, because there are 12 inches in a foot. So:
120,785 in. lbs divided by 12 in/ft = 10,065 foot-pounds L = 10′ (given). M = wL2/8. By transposition: w = 8M/L2 Substituting for M and L: w = 8(10,065 ft lbs)/ioo ft2 = 805 lbs/ft
That is: 805 pounds per linear foot. We haven’t got pounds per square feet quite yet. If rafters were on 12-inch centers, they could support 805 pounds per square foot (3,930 kilos per square meter). A linear foot would translate to a square foot in this special case. But our example calls for rafters on 30-inch centers, so we need to make the following adjustment:
i2"/sq. ft. divided by 30" = 0.4 ft.(8o5 lbs/ft) = 322 PSF allowable
Think of it this way: There are only 40 percent (0.4) as many rafters on 30- inch centers as on 12-inch centers. As the impact of frequency is a direct proportional relationship to strength, the rafters on 30-inch centers will support only 40 percent of the load, everything else remaining the same.
The specified rafters, on simple span, will easily support the 185 PSF required.
Now lets try it on a double span. We’ll use 20-foot-long rafters, supported at each end, but also at the middle by a girder.
2. Calculating roof load for bending for rafters, double-span. (That is,
all rafters are about twenty feet long, and supported at midspan by a
girder.)
Maximum allowable bending moment (M) = 10,065 foot pounds, from calculation (1) above.
Mx = Bending moment at the two midspans on a double-span beam
Mx = 9WLY128 (from formulas above)
W = 128 Mx /9L1 w = 128(10,065 ft. lbs.)/9(io ft)2 = 1431 lbs./ft
Again, this is “pounds per linear foot.” We make the same adjustment that we made at the end of calculation (1) above:
i2"/sq. ft divided by 30" = 0.4 ft.(i,43i lbs/ft) = 572 PSF allowable
Using a single 20-footer, supported halfway, increases bending strength by quite a bit, but this value is far stronger than it needs to be. Now, lets test rafters for shear.
3. Calculating roof load for shear on simple-span.
fv = 95 psi (pounds/square inch), given above for the same grade of Douglas Fir
A = bd = 5"(10") = 50 inches squared (In this case, the same as “square inches.”)
fv = 3V/2A. By transposition: V = 2Afv /3 = 2(50 in2)(95 lbs)/3(in2) = 3,167 pounds maximum allowable (V is “total shear allowable”)
V = wL/2. So, w =2V/L = 2(3,167 lbs)/io feet = 633 pounds per (linear) foot
But, again, rafters are not on 12" centers, but are actually 30 inches o. c. Making the adjustment: 12"/30" = 0.4 0.4(633) = 253 PSF allowable, another good strong number.
4. Calculating roof load for shear on a double-span rafter.
Maximum allowable shear (V) = 3,167 pounds from calculation (3) above. Shear at ends (Rj and R3): V = 3wL/8. Transposed: w = 8V/3L W = 8(3,167 pounds)/3(io feet) = 845 pounds per lineal foot Rafters are 30 inches o. c., so: = 0.4; 0.4(845) = 338 pounds per
square foot
That is the shear strength at the ends, at Rt and R3. But, at R2, the center support, the situation is a little different:
Shear at middle (R2): V = 5WL/8. Transposed: w = 8V/5L W = 8(3,167 pounds)/5(io feet) = 507 pounds per lineal foot Rafters are 30 inches o. c., so: = 0.4; 0.4(507) = 203 PSF, still more
than the 185 PSF foot required.
Now let’s do the girders, and we’ll just do them for single-span because 20- foot-plus eight-by-twelve girders are really a bit extreme. Plus, as we know, they will not only be easier to install as two io-footers, but the shorter pieces will actually be stronger on shear.
5. Calculating roof load for bending on the single span 8- by 12-inch Douglas fir girders of this example. The load from the rafters is symmetrically placed along the girder at regular 30-inch spacings, so it is reasonable to use the same formulas we used for single-span rafters.
S = bd’/6 = (8")(i2")2/6 = 192 in3 (Section modulus is measured in “inches cubed”)
fb = 1450 psi (pounds/square inch), given above for Douglas Fir, Inland Region, Common Structural
S = M/fb. By transposition: M = S(f^) M = 192^(1,450 lb/in1) = 278,400 in. lbs
This is the bending moment in “inch pounds”. To derive the more convenient “foot pounds,” we need to divide by 12 in/ft, because there are 12 inches in a foot. So:
278,400 in. lbs divided by 12 in/ft = 23,200 foot pounds
L = io’ (given) M = wL2/8. By transposition: w = 8M/L2
Substituting for M and L: w = 8(23,200 ft lbs)/ioo ft2 = 1,856 pounds per linear foot
The girder can support 1,856 pounds per linear foot, or 18,560 pounds in all, if the load is fairly constant along its length. But for what portion of the roof is the girder responsible? Look again at Fig. A2.1. The area AB is the area for which girder A-В is responsible. Area CD is part of the area carried by the girder C-D. Area W is carried by the block wall. The two areas labeled SR are carried by the special rafters labeled Y and Z. Y and Z are special because their loads are carried directly down through the girders to the posts, adding no bending stresses to the girder. The area AB is 10 feet by 7.5 feet or 75 square feet. So, the total allowable carrying capacity of the girder (18,560 pounds in all) divided by the square footage for which it is responsible (75 square feet) results in the allowable load per square foot, assuming an equally distributed load. 18,560 pounds/75 SF = 247.5 PSF. Still a good number, as it is higher than 185 PSF. Now, what about girders on shear?
6. Calculating roof load for shear on the single span 8” by 12" Douglas fir girders of this example. The load from the rafters is symmetrically placed along the girder at regular 30-inch spacings, so it is reasonable to use the same formulas we used for single-span rafters.
fv = 95 psi (pounds/square inch), given above for the same grade of Douglas Fir
A = bd = 6"(12") = 96 inches squared (In this case, the same as “square inches.”)
fv = 3V/2A. By transposition: V = 2Afv /3 = 2(96 in1) (95 lbs)/3 (in1) = 6,080 pounds maximum allowable (V is “total shear allowable”)
To get the shear strength at the ends of a single-span rafter, use:
V = wL/2 So, w =2V/L = 2(6,080 lbs)/io feet = 1,216 pounds per (linear) foot, or 12,160 pounds over 10 feet.
Again, the area for which girder A-В is responsible is area AB, or 75 SF.
12,160 pounds divided by 75 SF results in 162.1 PSF, which is less than the desired carrying capacity of 185 PSF for the earth roof described. It doesn’t look good. However, if we consider that the true girder clear span (between posts) is actually 9 foot 4 inches and substitute 9 foot 4 inches (9.333 ) for 10 feet in w = 2V/L, we get w = 1,303 pounds per linear foot, or 13,030 over 10 feet. Divided by 75 SF results in 173.7 PSF, closer, but still a little short of the mark. What can we do? Shear, unlike bending, is a direct linear relationship. The shortfall can be made up in variety of ways. These will all work:
A. Beef the girders up to 9 inches wide. Now A = 108 square inches instead of 96 square inches. This change increases the cross-sectional area of the girder — and its shear strength — by 12.5 percent because 12/96 = .125. Now, 173.7 PSF times 1.125 equals 195.4 PSF, so we’re good again.
B. Use a wood with a unit stress for horizontal shear at least 10 percent greater than the 95 psi for Douglas Fir (Inland Region, Common Structural). Any wood with an (fv) of at least 105 psi would do nicely.
C. Shorten the girder clear span by 7 inches to 8 foot 9 inches (8.75′). This yields 185.3 PSF, which is fine, as there are great safety factors built into these calculations. Just work to the numbers. You don’t have to add an additional safety factor.
D. If you want to keep the plan as designed, you could always decrease the load by about 12 PSF, down to 173 PSF. Eliminate 1.2 inches of earth or crushed stone. Is this cheating? In point of fact, the stone and earth layers at Earthwood are really about 8.5 inches total, not 10 inches, so our load here is probably about 170 PSF. This is enough to maintain our living roof.
Incidentally, using a 20-foot girder, supported half way, weakens the plan unacceptably in terms of shear strength for the girders. While shear strength increases at the ends to 218 PSF, it decreases over the center support to 130 PSF. Strange, but true. See Fig. 2.10 and the nearby commentary in Chapter 2 under the heading Shear and Shear Failure.
Disclaimer: The author is not an engineer. Use these exercises as a point of beginning, to get you into the ballpark. Always have your plan checked by a qualified structural engineer.
[1] Birch, Yellow. Hard and heavy. Can be stronger than red oak, but can be hard to work. Has a nice wintergreen aroma.
[2] Oak, White. The classic hardwood for timber framing, white oak is strong, durable, and decay resistant. It shrinks a lot, but in exposed rafters, joists, and girders, shrinkage is not really a problem. Sobon and Schroeder (1984) say it is very workable for traditional timber framing, but ten years later, Sobon (1994) says it is “more difficult to work than red oak or beech.” My personal experience is limited to making a few chainsaw cuts to join a ten-by-twelve white oak girder over a couple of eight-by-eight white oak posts. This is not a problem when the timbers are still fairly young. Once hardwoods are fully seasoned, sparks will fly off your chain!
[3] Pine, Red or Norway. Similar strength characteristics as white pine, but in my experience at Earthwood, the red pine twists a lot more than the
[4] The Granberg Mini-Mill. Similar to the Beam Machine, except that it comes with a 12-foot metal guide rail to fasten to a two-by-six plank (not provided), and an extra handle and guide assembly to help pull the
[5] Logosol Timber Jig. My editor for this book, Richard Freudenberger, tested this chainsaw attachment, similar to the Basic Alaskan Mills, and wrote a comprehensive report for BackHome magazine’s September/ October, 2003 issue. In the article, Richard says, “At 5^2 pounds, the Timber Jig is light enough to be carried into the woods with the saw. Yet if you wanted to set up a permanent work site to cut timbers or planks for a building project, it would be a simple matter to make a timber log table to support your logs at a comfortable working height.” Using an aged Husqvarna saw with a displacement of about five cubic inches, and a
[6] Better Built Ripsaw. This mill is also driven by a chainsaw head, but the bar and chain are replaced with a mounted bandsaw mill. In an article in Independent Sawmill and Woodlot Management magazine (August/ September, 2003), author Dave Boyt speaks well of this “simple and economical chainsaw-powered bandmill.” Although very much less expensive than full-sized portable sawmills, the $1,489 cost — plus the chainsaw — may not justify itself in a single project. However, it might be a very good investment for someone who anticipates additional homesteading projects in the future, or simply wants to add value to trees on the woodlot which need to be thinned.
[7] TimberLok™ screws are made by Olympic Manufacturing Group, Inc. listed in Appendix C. They come in a variety of lengths, with the six-, eight-, and ten-inch (15.2-, 20.3-, and 25.4-centimeter) ones the most useful for timber framing applications. Among the advantages over heavier shank screws and large nails, such as log cabin spikes, is that the TimberLok™ screws install faster and require no pre-drilling; they countersink into the beam; they have a corrosive resistant coating that also helps them grip; and they are easily removable. All TimberLok™ screws have a shank diameter of three-sixteenth inch, and a thread diameter of one-quarter inch. For the long screws, it is recommended to use a high-torque, low (450) rpm drill. Olympic supplies a five-sixteenths inch (8 millimeter) hex head bit with each box of screws. My local supplier sells a box of 50 ten-inch TimberLok™ screws for $28.
GRK Canada, Ltd (also listed in Appendix C), makes an even higher-quality — albeit more expensive — screw of a similar kind.






 Following are some views (Figures 5.41-5.45) and details of the completed sunroom.
Following are some views (Figures 5.41-5.45) and details of the completed sunroom.
 Jaki and I are glad that we have gained a beautiful new room as a result of this book… realizing that we wouldn’t have built it otherwise! In case you’re curious, the materials cost was about $4,000, or $20 per square foot. We also spent $250 on labor. And we also renewed the downstairs solar room at the same time, another 200 square feet, so were quite pleased with the cost. Larger buildings could cost less per square foot, particularly as our sunroom is heavy on windows ($1,243 for five) and an exterior door ($338), expensive items. I believe that a timber-frame home, using techniques described in this book, combined with some sort of natural infilling (cob, cordwood, straw bale, wattle-and-daub, etc.) can still be built today for a materials cost of $15 to $25 per square foot, depending on where you build and how good you are at scrounging materials.
Jaki and I are glad that we have gained a beautiful new room as a result of this book… realizing that we wouldn’t have built it otherwise! In case you’re curious, the materials cost was about $4,000, or $20 per square foot. We also spent $250 on labor. And we also renewed the downstairs solar room at the same time, another 200 square feet, so were quite pleased with the cost. Larger buildings could cost less per square foot, particularly as our sunroom is heavy on windows ($1,243 for five) and an exterior door ($338), expensive items. I believe that a timber-frame home, using techniques described in this book, combined with some sort of natural infilling (cob, cordwood, straw bale, wattle-and-daub, etc.) can still be built today for a materials cost of $15 to $25 per square foot, depending on where you build and how good you are at scrounging materials.
 rafter detail.
rafter detail.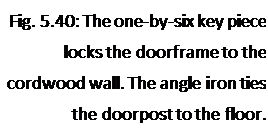
 Wood finishing. We sanded and varnished the window surrounds, and the posts and girders, but not the five – by-ten rafters. I used my trusty Makita 5"disk sander, #80 grit paper, to finish the timbers, some before construction, and some, as an afterthought, in situ. In retrospect, it would have been easier and more pleasant to do this sanding before installation. A belt sander is another option, but use a dust mask in either case. And listen to Mark Powers, one last time:
Wood finishing. We sanded and varnished the window surrounds, and the posts and girders, but not the five – by-ten rafters. I used my trusty Makita 5"disk sander, #80 grit paper, to finish the timbers, some before construction, and some, as an afterthought, in situ. In retrospect, it would have been easier and more pleasant to do this sanding before installation. A belt sander is another option, but use a dust mask in either case. And listen to Mark Powers, one last time:
 In the previous chapter, I told of the double-roof system, with false or secondary rafters over the real ones, and insulation as the filling of a plank sandwich. But the new sunroom extends the shallow 1:12 slope of the main house, and we wanted to continue out with the earth roof.
In the previous chapter, I told of the double-roof system, with false or secondary rafters over the real ones, and insulation as the filling of a plank sandwich. But the new sunroom extends the shallow 1:12 slope of the main house, and we wanted to continue out with the earth roof.
 Fig. 5.38: We installed 4 inches of Dow Styrofoam™, an extruded polystyrene, over the membrane.
Fig. 5.38: We installed 4 inches of Dow Styrofoam™, an extruded polystyrene, over the membrane.
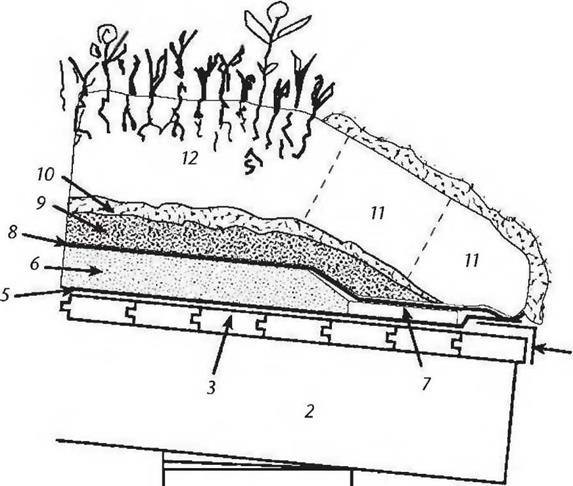
 7" to 8" topsoil, planted.
7" to 8" topsoil, planted. When the room was completed,
When the room was completed, Notice, in Fig. 5.33, that the original red pine rafter twisted slightly after construction, as red pine is inclined to do. I was able to straighten the rafter extension by making a biased cut out of the new rafter. This made for a tricky chainsaw cut. The key to success in this sort of thing is to mark the angle correctly on the piece to be cut. And the key to marking it correctly is to double – and triplecheck your angles and measurements. As I tend towards a slight dyslexia on this sort of thing, I would explain what I was doing to willing ears such as Rohan’s. He picks up quickly on wooly-minded thinking.
Notice, in Fig. 5.33, that the original red pine rafter twisted slightly after construction, as red pine is inclined to do. I was able to straighten the rafter extension by making a biased cut out of the new rafter. This made for a tricky chainsaw cut. The key to success in this sort of thing is to mark the angle correctly on the piece to be cut. And the key to marking it correctly is to double – and triplecheck your angles and measurements. As I tend towards a slight dyslexia on this sort of thing, I would explain what I was doing to willing ears such as Rohan’s. He picks up quickly on wooly-minded thinking.

 Each plate would require eight half-inch by з^-іпсії (1.2- by 9.0- centimeter) hex-headed lag screws. Six times eight is 48. It was quite a bit cheaper to buy two boxes with 25 screws per box than to buy 48 pieces out of the bin. So I have two left over.
Each plate would require eight half-inch by з^-іпсії (1.2- by 9.0- centimeter) hex-headed lag screws. Six times eight is 48. It was quite a bit cheaper to buy two boxes with 25 screws per box than to buy 48 pieces out of the bin. So I have two left over.


 This sturdy chain kit can replace your circular saw blade in a few minutes, and enables you to make deep accurate crosscuts through beams up to a foot thick. Think of the accuracy and convenience of a circular saw, combined with the depth of a chainsaw. It can even be used to do minor "saw milling," if you need to rip an inch or two off the edge of a beam. (For major saw milling, use one of the chainsaw mills described in Chapter 3.)
This sturdy chain kit can replace your circular saw blade in a few minutes, and enables you to make deep accurate crosscuts through beams up to a foot thick. Think of the accuracy and convenience of a circular saw, combined with the depth of a chainsaw. It can even be used to do minor "saw milling," if you need to rip an inch or two off the edge of a beam. (For major saw milling, use one of the chainsaw mills described in Chapter 3.)
 cross-sections.
cross-sections.
 After all three girders were set in place, we adjusted their positions slightly with a heavy hammer, sliding them this way and that until we were happy with the way they sat and joined each other. Small wooden shingle shims can be used as necessary to take any wobbles out. Then I toe-screwed up through the posts into the underside of the girders, using two screws at each side of a post. Fig. 5.32. I made a mistake at this point that you can avoid. I should have fastened the top sides of the girders together with truss plates, as I had done many times before. I either forgot to do this, or felt it wasn’t necessary, or thought that the truss plates might get in the way of rafters later on; I really don’t remember. (And excuses are like belly buttons; everybody has one.)
After all three girders were set in place, we adjusted their positions slightly with a heavy hammer, sliding them this way and that until we were happy with the way they sat and joined each other. Small wooden shingle shims can be used as necessary to take any wobbles out. Then I toe-screwed up through the posts into the underside of the girders, using two screws at each side of a post. Fig. 5.32. I made a mistake at this point that you can avoid. I should have fastened the top sides of the girders together with truss plates, as I had done many times before. I either forgot to do this, or felt it wasn’t necessary, or thought that the truss plates might get in the way of rafters later on; I really don’t remember. (And excuses are like belly buttons; everybody has one.)