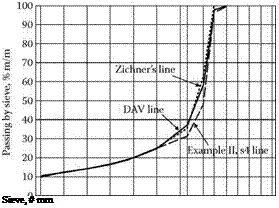
Zichner’s and DAV’s SMA versus 30-20-10 Rule
The 30-20-10 rule has more or less rigid proportions of gradation (expressed by
amounts passing through selected sieves). Zichner proposed the amount of coarse
a
![]()
![]()
![]()
![]()
 a
a
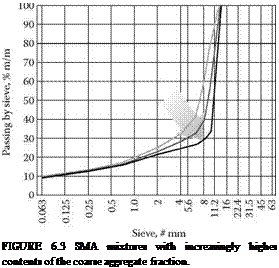
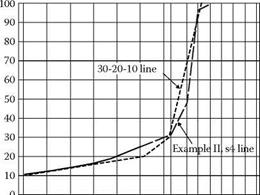
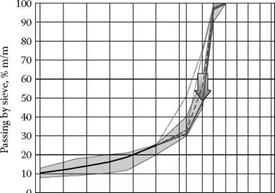
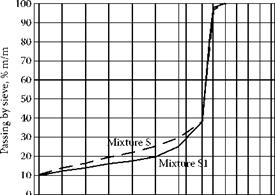
FIGURE 6.9 An SMA mix of Example II, Stage 4, compared with the line of the 30-20-10 rule.
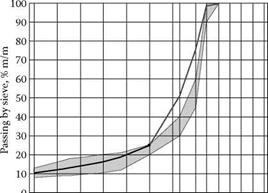
aggregates over a very wide range (65-80%), with a recommendation for 70-75%. His MASTIPHALT (SMA 0/12.5, mm) with 75% of grains larger than 2 mm has a gentle gap gradation with also more or less fixed proportions. There is no doubt that the 30-20-10 rule creates quite different mixtures than those created according to Zichner’s ideas. The other issue is with DAV’s proportions (Table 6.10) because these express the proportions between aggregates inside the coarse fraction. Hence the proportions mentioned can be applied to the amount of coarse aggregates fraction within the permitted range (e. g., 70-80%). In Figure 6.8 we compared the DAV line applied with a fixed 75% of coarse aggregates as we designed in Example II. Now we can evaluate the DAV proportions applied to a new content: 80% of coarse aggregates (similar to the 30-20-10 rule). After calculation of the gradation larger than the 2.0 mm sieve, according to DAV rules we can see grading curves as shown in Figure 6.10. The final assessment of the 30-20-10 rule line is slightly below the extreme line permitted by DAV proportions at 80% of coarse aggregate fraction. As is the case in Germany, there is a trend to decrease the amount of coarse aggregate content to 73-76% (Druschner, 2005). Taking into account this assumption, the 30-20-10 rule line is too low.
One can see in Figure 6.10 that the latest German regulations TL Asphalt-StB 07 for SMA 11S requires 35-45% of material passing a 5.6 mm sieve. It shows that Zichner’s or DAV’s proportions (for 70-76% of stones) are still in use.
6.3.2.2.2 Summary of Example II
The following is a list of the conclusions drawn from analyzing Example II: [24]
 |
FIGURE 6.10 Comparison of SMA gradations: 30-20-10 rule (solid line) and DAV lines for 70% and 80% of coarse fraction (dotted lines). The points show gradation limits in coarse fraction established in the newest German TL Asphalt-StB 07 for SMA 11S.
• The ratios of the coarse aggregate fractions cannot be even because this causes a loss of the necessary discontinuity of gradation.
• Quantities of the finest grains in the coarse fraction should be reduced when composing the total coarse aggregate fraction.
• The content of grains larger than 2 mm (the coarse aggregate) in an SMA aggregate mix do not explicitly determine its aggregate skeleton and properties; aggregates passing the 5 or 8 mm sieves are also needed.
• Increasing the quantity of particles larger than 5 mm leads to opening the mix; this effect is even more noticeable when raising the content of particles larger than 8 mm.






 10
10

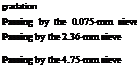
 component of aggregate mixture content, (m/m)
component of aggregate mixture content, (m/m)
 0
0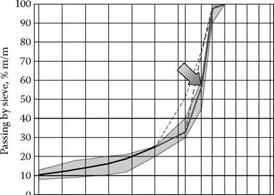 0
0
 0
0 content, (m/m) comments
content, (m/m) comments
 0
0