Having constructed an optimization model, one must choose an optimization technique to solve the model. The way that one solves the problem depends largely on the form of the objective function and constraints, the nature and number of variables, the kind of computational facility available, and personal taste and experiences. Mays and Tung (1992) provide a rather detailed discussion on linear programming, dynamic programming, and nonlinear programming techniques. In this subsection, brief descriptions are given to provide
readers with some background about these techniques. A list of applications of various optimization techniques to hydrosystems engineering problems can be found elsewhere (Mays and Tung, 2005).
Linear programming (LP). LP has been applied extensively to optimal resource allocation problems. When the system under study is linear, LP models also can be used for parameter identification and system operation. By the name of the technique, an LP model has the basic characteristic that both the objective function and constraints are linear functions of the decision variables. The general form of an LP model can be expressed as
n
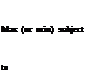 xo = ^ CjXj (8.3a)
xo = ^ CjXj (8.3a)
j=i
n
‘^a. ijXj = bi i = 1,2,…, m (8.3b)
j=1
Xj > 0 j = 1, 2,…, n (8.3c)
where the Cj’s are the objective function coefficients, the aij’s are called the technological coefficients, and the bi’s are the right-hand-side (RHS) coefficients. An LP model can be expressed concisely in matrix form as
|
Max (or min)
|
xo = ctx
|
(8.4a)
|
|
subject to
|
Ax = b
|
(8.4b)
|
|
x > 0
|
(8.4c)
|
where c is an n x 1 column vector of objective function coefficients, x is an n x 1 column vector of decision variables, A is an m x n matrix of technological coefficients, b is an m x 1 column vector of the RHS coefficients, and the superscript t represents the transpose of a matrix or vector. Excellent books on LP include Winston (1987), Taha (1987), and Hillier and Lieberman (1990).
The commonly used algorithm for solving an LP model is the simplex method developed by Dantzig (1963). Since its conception, the method has been used widely and considered as the most efficient approach for solving LP problems. The simplex algorithm, starting at an initial feasible solution to the LP model, searches along the boundary of a problem’s feasible space to reach the optimal solution. The method has been applied to solve large problems involving thousands of decision variables and constraints on today’s computers. Computer codes based on the simplex method are widely available. Some of the well-known LP software includes GAMS (general algebraic modeling system) by Brooke et al. (1988) and LINDO (linear, interactive, and discrete optimizer) by Schrage (1986), for which PC versions of the programs are available. For LP
models, because of the convexity of the feasible region, the solution obtained is a global optimum.
Two additional methods for solving LP problems have been developed that apply different algorithmic strategies (Khatchian, 1979; Karmarkar, 1984). In contrast to the simplex algorithm, Khatchian’s ellipsoid method and Karmarkar’s projective scaling method seek the optimum solution to an LP problem by moving through the interior of the feasible region.
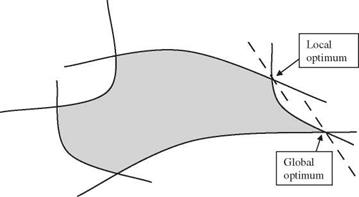
Nonlinear programming (NLP). A nonlinear programming model has the general format of Eqs. (8.1a-c) in which either the objective function f (x) or the constraints g (x) or both are nonlinear. In an NLP problem, the convexity of the feasible space defined by the nonlinear constraints g (x) is generally difficult to assess. As a result, the solution obtained by any NLP algorithm cannot guarantee to be globally optimal. Detailed description for solving NLP problems can be found in Edgar and Himmelblau (1988), Fletcher (1980), McCormick (1983), and Gill et al. (1981).
Basically, algorithms for solving NLP problems are divided into two categories: unconstrained and constrained algorithms. Unconstrained NLP algorithms solve Eq. (8.1a) without considering the presence of constraints. They provide the building blocks for the more sophisticated constrained NLP algorithms. Consider an unconstrained NLP problem
Minimize f (x) x є Kn (8.5)
in which Kn is an n-dimensional real space. Assume that f (x) is twice differentiable; the necessary conditions for x* to be a solution to Eq. (8.5) are (1) Vxf (x*) = 0 and (2) V| f (x*) = H(x*) is semipositive definite in which Vxf = (d f /д x1, d f /д x2,…, d f /dxn)t, agradient vector of the objective function and Vx2 f = (д2 f /дxiдxj) is an nx nHessian matrix. The sufficient conditions for an unconstrained minimum x * are (1) Vxf (x *) = 0 and (2) Vxf (x *) = H (x *) is strictly positive definite.
In theory, the solution to Eq. (8.5) can be obtained by solving Vxf (x*) = 0, which involves a system of n nonlinear equations with n unknowns. This approach has been regarded as indirect because it backs away from solving the original problem of minimizing f (x). Furthermore, numerical iterative procedures are required to solve the system of nonlinear equations which tend to be computationally inefficient. Therefore, the general preference is given to those solution procedures which directly attack the problem of optimizing the objective function. Like the LP solution procedure, direct solution methods, during the course of iteration, generate a sequence of points in the solution space that converge to the solution of the problem by the following recursive equation:
x(r+1) = x(r} + в(r}d(r} r = 1,2,… (8.6)
in which the superscript (r) represents the iteration number, x is the vector of the solution point, d is the vector of the search direction along which the objective function f (x) is to be minimized, and в is a scalar, called the step size, that minimizes f (x(r) + в(r)d(r)). This procedure is called the line search or one-dimensional search. Several unconstrained NLP algorithms have been developed, and they differ by the way the search directions are determined during the course of iteration. Mays and Tung (1992, p. 136) summarize the search directions of various methods.
Without losing generality, consider a nonlinear constrained problem stated by Eq. (8.1) with no bounding constraints. Note that the constraints Eq. (8.1b) are all equality constraints. Under this condition, the Lagrangian multiplier method can be applied, which converts a constrained NLP problem to an uncon – strainted one by an augmented objective function called the Lagragian. That is, Eqs. (8.1a-b) can be written as
Minimize L(x, X) = f (x) + Xіg(x) (8.7)
in which L(x, X) is the Lagrangian function, X is the vector of m Lagragian multipliers, and g(x) is the vector of constraint equations. The new objective function L(x, X) involves n + m decision variables. The necessary condition and sufficient conditions for x* to be the solution for Eq. (8.7) are
1. f (x*) is convex, and g(x*) is convex in the vicinity of x*.
2. VXL(x*, X) = 0.
3. VxL(x*, X) = g(x*) = 0.
4. X’s are unrestricted in sign.
Solving conditions 2 and 3 simultaneously yields the optimal solution to Eq. (8.7).
The most important theoretical results for the NLP problem are the Kuhn – Tucker conditions, which can be derived easily by using the Lagrangian method for the general NLP problem, as stated in Eq. (8.1a-c). These conditions must be satisfied at any constrained optimum, local or global, of any LP or NLP problem. They form the basis for the development of many computational algorithms.
Several NLP computer codes are available commercially. They are the GRG2 (generalized reduced gradient 2) developed by Lasdon and his colleagues (Lasdon et al., 1978; Lasdon and Waren, 1978); (2) GINO (Liebman et al., 1986); (3) MINOS (modular in-core nonlinear optimization system) by Mautaugh and Saunders (1980, 1983), and (4) GAMS-MINOS, a link for GAMS and MINOS. Microsoft Excel SOLVER implements GINO in a spreadsheet working environment.
Dynamic programming (DP). Before performing the optimization, it is sometimes desirable to make some changes of variables and transformations so that the model can be solved more efficiently. However, one must keep in mind that such transformations should completely preserve the properties of the original problem (model) so that the transformed model will yield the optimal solution to the original problem. Basically, DP is such a transformation that takes a sequential or multistage decision process containing many interrelated decision variables and converts it into a series of single-stage problems, each containing only one or a few variables. In other words, the DP technique decomposes an n-decision problem into a sequence of n separate but interrelated single-decision subproblems. Books that deal with DP are Dreyfus and Law (1977), Cooper and Cooper (1981), and Denardo (1982).
To describe the general philosophy of the DP technique, consider the following resource allocation problem (Tung and Mays, 1992). Suppose that one wishes to allocate funds to three water development projects, A, B, and C, to maximize the total revenue. Each development project consists of several alternative configurations that require different funding levels and yield different revenues. Owing to the budget limitation, the total available funds for the entire development are fixed. If the number of alternatives for each project is not too large, one probably can afford to enumerate all possible combinations of project alternatives exhaustively to identify the optimal alternatives for the entire project development. This brute-force exhaustive enumeration approach possesses three main shortcomings: (1) It would become impractical if the number of alternative combinations is large, (2) the optimal course of action cannot be verified, even it is obtained in the early computations, until all the combinations are examined, and (3) infeasible combinations (or solutions) cannot be eliminated in advance.
Using the DP technique, one considers the selection of alternatives within each project individually without ignoring the interdependence among the projects through the total available budget. Since the total funds are limited, the amount available to each project depends on the allocations to the other projects. Whatever funds are given to project A and project B, the allocation to the remaining project C must be made to optimize its return with respect to the remaining capital. In other words, the optimal allocation to project C is conditioned only on the available funds for project C after allocations to project A and project B are made. Since one does not know the optimal allocations to project A and project B, the optimal allocation and the corresponding revenue from project C must be determined for all possible remaining funds after allocations to project A and project B have been made. Furthermore, whatever amount is allocated to project A, the allocations to project B and project C must be made optimal with respect to the remaining funds after the allocation is made to project A. To find the optimal allocation to project B, one finds the allocation maximizing the revenue from project B together with the optimal revenue from project C as a function of remaining funds from the allocation to project B. Finally, the optimal allocation to project A is determined, to maximize the revenue from project A plus the optimal revenue from both project B and project C, as a function of the funds remaining after the allocation to project A.
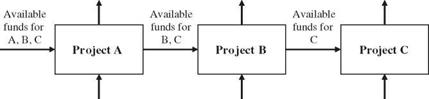
This description of the DP algorithm applied to a budget allocation example can be depicted schematically as Fig. 8.3, from which the basic elements and terminologies of a DP formulation are defined.
|
Return Return Return
from A from B from C
Decision Decision Decision
for A for B for C
Figure 8.3 Dynamic programming diagram for budget allocation example.
|
1. Stages (n) are the points in the problem where decisions are to be made. In the funds allocation example, each different project represents different stages in the DP model.
2. Decision variables (dn) are courses of action to be taken for each stage. The decision in each stage (project) is the alternative within the project to be selected for funding. The number of decision variables dn in each stage is not necessarily equal to one.
3. State variables (Sn) are variables describing the state of a system at different stages. A state variable can be discrete or continuous, finite or infinite. Referring to Fig. 8.3, at any stage n, there are the input state Sn and the output state Sn+1. The state variables of the system in a DP model have the function of linking between succeeding stages so that when each stage is optimized separately, the resulting decision is automatically feasible for the entire problem. Furthermore, it allows one to make optimal decisions for the remaining stages without having to check the effect of future decisions on the decisions made previously. Given the current state, an optimal policy for the remaining stages is independent of the policy adopted in the previous stages. This is called Bellman’s principle of optimality, which serves as the backbone of the optimization algorithm of the DP technique.
4. Stage return (rn) is a scalar measure of effectiveness of the decision made in each stage. It is a function of input state, output state, and the decision variable of a particular stage. That is, rn = r (Sn, Sn+1, dn).
5. State transition function (t„) is a single-valued transformation that expresses the relationships between input state, output state, and decision. In general, through the stage transition function, the output state Sn+1 at any stage n can be expressed as the function of input state Sn and the decision dn as
Sn+1 = tn(Sn, dn) (8.8)
The solution begins with finding the optimal decision for each possible state in the last stage (called the backward recursive) or in the first stage (called the forward recursive). Usually, one can exchange the sequence of the decision-making process. Hence which end to begin will be trivial. A recursive relationship that identifies the optimal policy for each state at any stage n can be developed, given the optimal policy for each state at the next stage n + 1. This backward-recursive equation, referring to Fig. 8.4, can be written as
f*(Sn) = optdn{rn(Sn, dn)} for n = N
= optdn {r n( Sn, dn) о f*+1[tn( Sn, dn)]} for n = 1,2,…, N – 1 (8.9)
in which о represents a general algebraic operator that can be +, -, x, or others.
The efficiency of an optimization algorithm is commonly measured by the computer time and storage required in problem solving. In the DP algorithm, the execution time mainly arises from the evaluation of the recursive formula, whereas the storage is primarily for storing the optimal partial return and the decision for each feasible state in each stage. DP possesses several advantages in solving problems involving the analysis of multiperiod processes; however, there are two major disadvantages of applying DP to many hydrosystems problems, i. e., the computer memory and time requirements. These disadvantages would become especially severe under two situations: (1) when the number of state variables is beyond three or four and (2) when DP is applied in a discrete fashion to a continuous state space. The problem associated with the second situation is that difficulties exist in obtaining the true optimal solution without having to considerably increase discretization of the state space.
Because of the prohibitive memory requirement of DP for multidimensional systems, several attempts have been made to reduce this problem. One such modification is the discrete differential DP (DDDP). The DDDP is an iterative DP that is specially designed to overcome the shortcomings of the DP approach. The DDDP uses the same recursive equation as the DP to search for an improved trajectory among discrete states in the stage-state domain in the vicinity of an initially specified or trail trajectory (Heidari et al., 1971). Instead of searching over the entire state-stage domain for the optimal trajectory, as is the case for DP, DDDP examines only a portion of the state-stage domain, saving a considerable amount of computer time and memory (Chow et al., 1975). This optimization procedure is solved through iterations oftrial states and decisions to search for optimal returns (maximum or minimum) for a system subject to the constraints that the trial states and decisions should be within the respective admissible domain in the state and decision spaces.
|
ri
f
|
|
Г2 1
|
|
Гп
|
|
Гn+1 1
|
|
rN
|
|
Stage
1
|
|
Stage
1
|
__ ^ …. _Sn^
|
Stage
n
|
Sn+1 —►
|
Stage n + 1
|
__ ^ ___ Sn ^
|
Stage
N
|
|
1
d1
|
|
1
d2
|
|
dn
|
|
1
dn+1
|
|
dN
|
|
Figure 8.4 Schematic diagram of dynamic programming representation.
|
General purpose computer codes for solving DP problems are not available commercially because most problems are very specific and cannot be cast into a general framework such as Eqs. (8.1a-c). Therefore, analysts often have to develop a customized compute code for a specific problem under consideration.
Global optimization techniques. To optimize a complex hydrosystem involving a large number of interrelated decision variables, it is generally difficult to be certain that the optimal solution can be obtained within a reasonable amount of time. In dealing with such “hard” problems, one could opt to obtain the optimal solution with the anticipation to consume a vary large amount of computational time using the optimization techniques previously mentioned or to reach a quick but good solution that is suboptimal through some approximate or heuristic algorithms. Simulated annealing (SA) and genetic algorithm (GA) are two types of high-quality general algorithms that are independent of the nature of the problem. Both SA and GA, by nature, are randomization algorithms that apply a local search based on stepwise improvement of the objective function through exploring the neighboring domain of the current solution. The quality of the local optimum can be strongly dependent on the initial solution, and in practice, it is difficult to assess the time needed to reach the global optimum. To avoid being trapped in a local optimum, local search algorithms can (1) try a large number of initial solutions, (2) introduce a more complex neighborhood structure to search a larger part of the solution space, and (3) accept limited transitions to explore the solution space in which the solution is inferior (Aarts and Korst, 1989).
Simulated annealing algorithms. The simulated annealing (SA) algorithms solve optimization problems by using an analogy to physical annealing process of decreasing temperature to lower energy in a solid to a minimum level. The annealing process involves two steps: (1) increasing the temperature of a heat bath to a maximum value at which the solid melts, and (2) decrease carefully the temperature of the heat bath to allow particles to arrange themselves in a more structured lattice to achieve minimum energy level. If the temperature of the heat bath decreases too rapidly (called quenching), the solid could be frozen into a metastable state in which the solid would be brittle. The connection between optimization and the annealing process was first noted by Pincus (1970) and formalized as an optimization technique by Kirkpatrick et al. (1983).
SA algorithms employ random search, which not only accepts solutions that improve the current solution but also accept solutions that are inferior with a specified probability according to the Metropolis criterion, that is,
where x-1 is the optimal solution in the r th iteration, x j +1 is the j th trial solution of the (r + 1)th iteration, f ( ) is the objective function value analogous
to the energy level of a solid, and T is the control parameter analogous to the temperature of the heat bath. As can be seen from Eq. (8.10), in a subsequent iteration a new trial solution yielding an objective function value that is a worse objective function value compared with the current optimum one will have lower (but not zero) probability of being accepted than a solution producing a better objective function value.
Implementation of the SA algorithm is remarkably easy, as shown in Fig. 8.5, which involves the following steps: (1) generation of possible solutions to explore
|
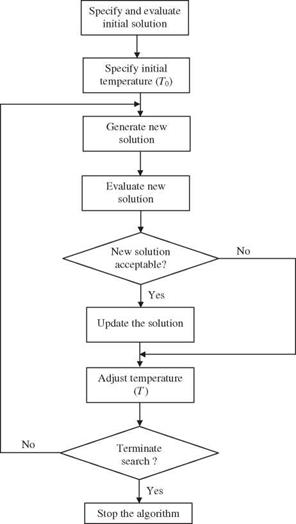
Figure 8.5 Algorithm of simulated annealing.
|
the solution space, (2) evaluation of the objective function, and (3) definition of the annealing schedule specified by the initial control parameter T0, decrement of control parameter AT, and convergence criteria. Mechanisms for generating trial solutions in each iteration involve introducing random changes with the intent to cover the solution domain to be searched. The domain of search generally changes with the iteration, and there are many ways to implement domain search (Vanderbilt and Louie, 1984; Parks, 1990).
Since SA algorithms only require objective function evaluation at each generated trial solution, computational efficiency of the entire process could become an important issue because implementation of the algorithms anticipates a large number of function evaluations. Many optimization problems in hydrosystems engineering involve objective functions whose values depend on physical constraints defined by complex flow simulations. In such cases, it is worthy of the effort to search and implement more computationally efficient procedures. To handle constraints in an SA algorithm, the simplest way is to reject the trial solution if it leads to a constraint violation. Alternatively, penalty function can be introduced to account for the constraint violations.
In implementation of the SA algorithm, T0 is generally set to be high enough to allow virtually all trial solutions to be accepted. It is analogous to having the temperature in the heat bath high enough to “melt” the solid. It is equivalent to the acceptance probability for T0 being close to 1. As the solution improves with the iterations, the control parameter T gradually decreases in value. The SA iteration is terminated when the control parameter T reaches a specified final value or the total number of trial solutions is reached. Alternatively, one can halt the algorithm if lack of improvement in the objective a function value is defined, which can be (1) no improvement can be found in all trial solutions at one control parameter and (2) acceptance ratio falls below a specified value.
Genetic algorithms. Genetic algorithms (GAs) are a class of computer-based search procedures that emulate the biologic evolution processes of natural selection and genetics. Since its introduction by Goldberg in 1983, this innovative search procedure has been applied widely for optimization in a wide variety of areas (Goldberg, 1989). GAs have been demonstrated to be robust search procedures that outperform the conventional optimization procedures, in particular for problems with high dimensionality, discontinuities, and noise.
Using GA for optimization, analogues are made between the properties of an optimization problem and the biologic process of gene selection and reproduction. The solution space for an optimization problem can be treated as the environment in which potential solutions can be considered as genes. The degree of fitness of each gene can be measured by the value of the objective function of an optimization problem. In each iteration of a GA search, several genes representing solutions are generated from the population. These genes compete for their survival based on their fitness: The one that is fitter is more likely to survive and influence the next generation. Through this competition, the population evolves to contain high-performance individuals. In a GA, iteration is represented by a generation, and decision variables are analogous to biologic genes and are represented by coded structures either in the form of a real number or binary codes. A point in the solution space is represented by a collection of genes, and the coded genes are juxtaposed to form an individual or chromosome.
Like any optimum-seeking algorithm, a GA requires the specification of an initial population (the first generation) of potential solutions. This can be done by random generation of a population or by specifying an initial solution. In the initial population, the fitness of an individual is evaluated with respect to the objective function. Those individuals with a high level of fitness will have higher chance being selected to produce offspring than those individuals with a lower level of fitness. The selection can be conducted in many different ways, such as stochastic universal sampling (Baker, 1987), which behaves like a roulette wheel with the slot size apportioned to each individual’s relative fitness in the population. The principle of the selection is to prefer better solutions to worse ones. This very feature of the selection procedure in a GA is similar to the Metropolis acceptance criterion of SA algorithms. The implementation of such selection procedure will prevent the solutions from being trapped at the local optimum.
On the completion of selection of individuals in a generation, individuals selected will mate to produce the population of the next generation. During the mating, biologic processes of gene crossover and mutation could take place. Again, fitness of individuals in the population of the new generation will be evaluated based on which selection and mating processes will be repeated. A schematic diagram of a GA is shown in Fig. 8.6. Through this repeated
|
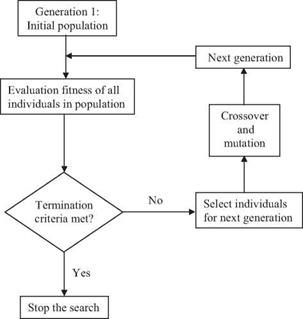
Figure 8.6 Schematic diagram of genetic algorithm.
|
fitness-selection-reproduction cycle, the population generated by the GA will evolve toward improved solutions.
Two main mechanisms are involved for those selected individuals to generate offspring in the next generation, i. e., crossover and mutation. Crossover allows information exchange between two chosen individuals forming the parents. In GA, crossover is done by randomly selecting positions in a chromosome of two individuals to swap their coded genes to produce the offspring. The rate of crossover has been suggested to be from 0.6 to 1.0 (Goldberg, 1989). Mutation then is a process by which new genetic materials can be introduced into the population. It is applied on a bit-by-bit basis, with the mutation rate specified by the user.







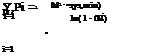

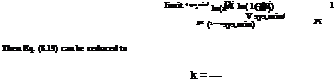
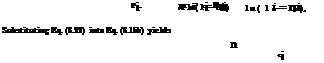
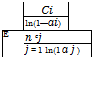
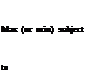 xo = ^ CjXj (8.3a)
xo = ^ CjXj (8.3a)