Basic concept
The basic concept of risk-based design is shown schematically in Fig. 8.9. The risk function accounting for the uncertainties of various factors can be obtained using the reliability computation procedures described in earlier chapters. Alternatively, the risk function can account for the potential undesirable consequences associated with the failure of hydrosystem infrastructures. For simplicity, only the tangible damage cost is presented herein.
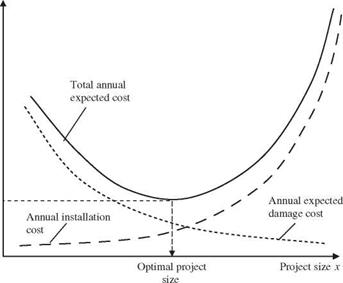
Risk costs associated with the failure of a hydrosystem infrastructure cannot be predicted accurately from year to year. A practical way is to quantify risk cost using an expected value on an annual basis. The total annual expected cost (TAEC) is the sum of the annual installation cost and annual expected damage cost, which can be expressed mathematically as
TAEC(x) = FC(x) x CRF + E(Dx) (8.29)
where FC is the first or total installation cost, which is the function of decision vector x defined by the size and configuration of the hydraulic structure, E(D x) is the annual expected damage cost associated with structural failure, and CRF is the capital recovery factor, which brings the present worth of the installation costs to an annual basis and can be computed as
CRF = (1 + i} T~T 1 (8.30)
i(1 + i)1
Annual cost
|
Figure 8.9 Schematic diagram of optimal risk-based design. |
with T and і being the expected service life of the structure and the interest rate, respectively.
In practice, the optimal risk-based design determines the optimal structural size, configuration, and operation such that the annual total expected cost is minimized. Referring to Fig. 8.6, as the structural size increases, the annual installation cost increases, whereas the annual expected damage cost associated with the failure decreases. The optimal risk-based design procedure attempts to determine the lowest point on the total annual expected cost curve. Mathematically, the optimal risk-based design problem can be stated as
Minimize TAEC(x) = FC(x) x CRF + E(Dx) (8.31a)
subject to gi (x) = 0 і = 1,2,…, m (8.31b)
where gi(x) = 0, і = 1, 2,…, m, are constraints representing the design specifications that must be satisfied.
In general, the solution to Eqs. (8.31a-b) could be acquired through the use of appropriate optimization algorithms. The selection or development of the solution algorithm is largely problem-specific, depending on the characteristics of the problem to be optimized. Section 8.4 describes an application of the optimal risk-based design to pipe culverts for roadway drainage.






Leave a reply