The optimization model defined by Eqs. (8.1a-c) is for a single-objective problem. On the other hand, multiobjective programming deals with problems involving several noncommensurable and often conflicting objectives simultaneously. Among the objective functions involved, no single one has an importance that is overwhelmingly dominant over all others. Under this circumstance, the ideological theme of optimality in the single-objective context is no longer appropriate.
Mathematically, a multiobjective programming problem can be expressed in terms of vector optimization as
Maximize f (x) = [ f 1(x), f 2(x),…, fM(x)] (8.2a)
subject to g(x) = 0 (8.2b)
in which f (x) is a vector of M objective functions, g(x) = 0 are vector of constraints, and x is a vector of decision variables.
The solution to a multiobjective programming problem is a best compromis — able solution according to the decisionmaker’s preference among the objectives and the noninferior solutions to the problem. A noninferior solution to a multiobjective programming problem is a feasible solution to which there is no other
|
(a) |
|
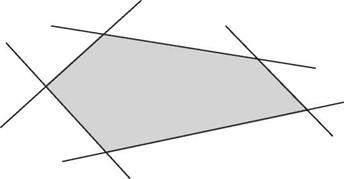
(b) Figure 8.1 Schematic diagrams of (a) convex and (b) non-convex spaces. |
feasible solution that will yield an improvement in one objective without causing degradation to at least one other objective (Cohon, 1978). The collection of such noninferior solutions allows the assessment of tradeoff among conflicting objectives.
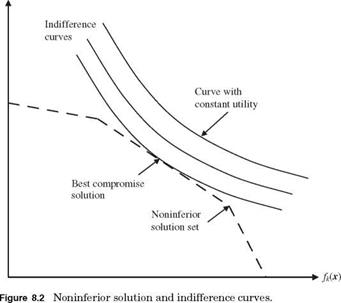
To obtain the solution to a multiobjective programming problem, the preference of the decisionmaker among the conflicting objectives must be known. Information concerning the decisionmaker’s preference is commonly called the utility function, which is a function of the objective function values. Geometrically, the utility function can be depicted as a series of indifference curves (Fig. 8.2). The utility of a decision maker will be the same for a combination of solutions that fall on the same indifference curve. The best compromise solution to a multiobjective programming problem is a unique set of alternatives that possesses the property of maximizing the decisionmaker’s utility, and the alternatives are elements of the noninferior solution set.
|
fj(x)
|
Many methods have been proposed to derive the solution to a multiobjective programming problem. Basically, they can be classified into two categories (Cohon, 1978): generating techniques and techniques incorporating knowledge of the decisionmaker’s preference. The purpose of generating techniques is to provide decisionmakers with information about the noninferior solution set or feasible tradeoff to the multiobjective problem. System analysts play the role of information providers and do not actively engage in decision making. On the other hand, techniques in the other category explicitly incorporate the decisionmaker’s preference to search for the best compromise solution. Detailed descriptions of various techniques for solving multiobjective problems can be found elsewhere (Cohon, 1978; Goicoechea et al., 1982; Chankong and Haimes, 1983; Steuer, 1986). Regardless of the approach to be used for solving a multiobjective programming problem, the basic solution technique is still one of single-objective optimization algorithms.
