Multiobjective stochastic waste-load allocation
The WLA problem, by nature, is a multiobjective problem involving several conflicting objectives. The treatment-equity constraint (Eq. 8.59c) is incorporated for the purpose of fairness. Without it, any attempt to maximize waste discharge (or to minimize treatment cost) could result in allocating large quantities ofwaste to the upstream users, whereas the downstream discharges could be required to treat their effluent at levels of maximum possible efficiency. This is especially true for slow-moving streams. Several articles have discussed the importance of equity considerations in WLA problems (Gross, 1965; Loucks et al., 1967; Miller and Gill, 1976; Brill et al., 1976).
In general, as the requirement for an equity measure (or fairness) is raised, the total waste discharge to the stream system would be reduced. This will be in direct conflict with the maximization of waste discharge associated with the minimization of treatment cost. Furthermore, from the preserving stream water-quality viewpoint, setting a higher water-quality standard is more desirable. However, such an objective cannot be achieved without increasing waste treatment cost. Therefore, the objectives of preserving water quality and of
enhancing economic efficiency are in conflict each other. Lastly, as the requirement of reliability in complying with the water-quality standard is raised, the total waste load that can be discharged expectedly would have to be reduced. Therefore, the task of solving WLA problems is multiobjective.
From the preceding discussions, four objective functions can be considered in WLA modeling: (1) maximization of the total waste load, (2) minimization of differences in treatment levels among waste dischargers, (3) maximization of allowable in-stream DO concentration, and (4) maximization of the water – quality standard compliance reliability. The first objective Z1 can be formulated as Eq. (8.59a), which is repeated here as
N
Maximize Z1 = (Bj + Dj)
j=i
For a stream system involving multiple waste dischargers, the difference in required treatment levels generally would vary. To collapse different values of equity measure into a single representative indicator, the worst case associated with the largest differences can be used. With that, the second objective can be expressed as
|
|
||
|
|
||
|
|
||

where 5max is a new decision variable for the equity measure representing the largest difference in treatment levels among waste dischargers.
The third objective considered is the maximization of the lowest allowable DO concentration level that should be maintained in the stream environment. This objective can be expressed as
![]() Maximize Z3 = DO^
Maximize Z3 = DO^
in which the new decision variable DOsmtdin is the minimum required DO standard in the stream.
Similar to the differences in treatment levels, the water-quality compliance reliability at different control points will not be uniform. To use a single representative measure of compliance reliability for the entire system, a conservative view of looking at the lowest reliability was applied. The objective is to maximize this lowest compliance reliability amin as
Maximize Z4 = amin = min[a1, a2,…, aM ] (8.71)
By the definitions of DO^^in and amin, the chance constraints for water-quality compliance (Eq. 8.59b) can be modified as
(8.72)
The corresponding deterministic equivalent of Eq. (8.72) can be expressed as
П ni
(®ij) Bj + E E (Vj Dj + DOmtdn j=1 j=1
+ Fz-1(amin)V(B, D)C (&i, П)(B, D) < Ri (8.73)
in which R i = DOsat – E (aoi).
Note that the original objective given in Eq. (8.71) is to maximize amin. However, under the assumption that the standardized left-hand sides of the water – quality constraints are continuous and unimodal random variables, the decision variable amin would have a strictly increasing relationship with Fz_1(amin). Therefore, maximization of amin is then equivalent to maximizing Fz_1(amin). By letting zmin = Fz_1(amin), Eq. (8.71) can be written as
Maximize Z4 = zmin (8.74)
Note that the decision variable zmin is unrestricted in sign. The objective of maximizing the lowest compliance reliability is equivalent to minimizing the highest water-quality violation risk.
The preceding multiobjective WLA problem can be solved by various techniques described in the references cited in Sec. 8.1.2. In the following, the constraint method is used by which the preceding multiobjective WLA problem is expressed as
![]() Maximize zmin
Maximize zmin
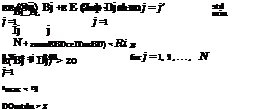 |
 |
subject to
and nonnegativity constraints for the decision variables, except for zmin. In Eqs. (8.75e-g), the right-hand sides Z, ZO, and Z3 are the values of the objective functions 1, 2, and 3, respectively, which are to be varied parametrically.
|
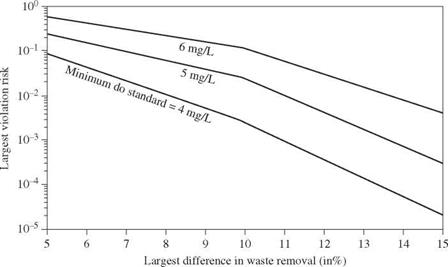
Figure 8.22 Tradeoff curves of various objectives in stochastic WLA problem with 4 mg/L minimum DO standard. (After Tung and Hathhorn, 1989.) |
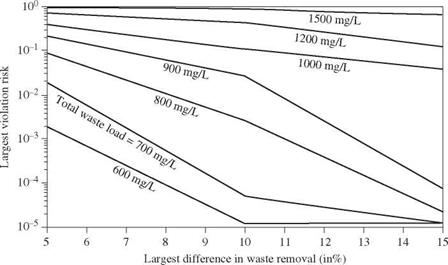
Using the same hypothetical stream system as shown in Fig. 8.21 and the corresponding data, the solution to this multiobjective WLA model by the constraint method yields a series of tradeoff curves among the various objectives. Figures 8.22 through 8.24 show the tradeoffs among three objectives for a given
|
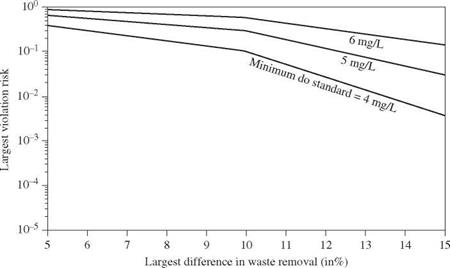
Figure 8.23 Tradeoff curves of various objectives in stochastic WLA problem with 5 mg/L minimum DO standard. (After Tung and Hathhorn, 1989.) |
|
Figure 8.24 Tradeoff curves of various objectives in stochastic WLA problem with 6 mg/L minimum DO standard. (After Tung and Hathhorn, 1989.) |
minimum DO standard concentration. As can be seen for a specified minimum DO standard and total waste load, the largest water-quality violation risk decreases as the maximum difference in treatment equity increases. An increase in the treatment equity measure by 5max implies a larger tolerance for the
|
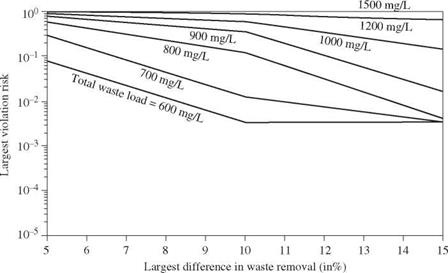
Figure 8.25 Tradeoff curves of the various objectives in stochastic WLA problem with total waste load fixed at 800 mg/L. (After Tung and Hathhorn, 1989.) |

|
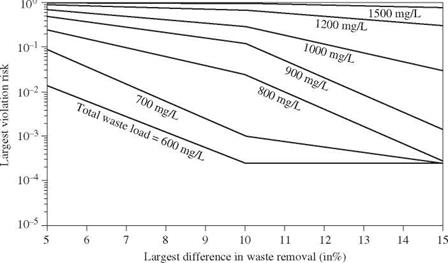
unfairness in the treatment requirement among waste dischargers. As the level of the minimum required DO standard is raised, the set of tradeoff curves moves upward. To show the tradeoffs for different minimum DO standard, Figs. 8.25 and 8.26 are plotted for the risk of water-quality standard violation, treatment equity, and water-quality standard while the total waste load to the stream system is fixed at some specified levels.






Leave a reply