Evaluations of annual expected flood damage cost
In risk-based and optimal risk-based designs of hydrosystem infrastructures, the thrust of the exercise, after uncertainty and risk analyses are performed, is to evaluate E( Dx) as the function of the probability density functions (PDFs) of loading and resistance, damage function, and the types of uncertainty considered.
Conventional approach. In conventional risk-based design, where only inherent hydrologic uncertainty is considered, the structural size x and its corresponding flow-carrying capacity qc, in general, have a one-to-one monotonically increasing relationship. Consequently, the design variables x alternatively can be expressed in terms of design discharge of the hydrosystem infrastructure. The annual expected damage cost, in the conventional risk-based hydraulic design, can be computed as
where qt is the deterministic flow capacity of a hydraulic structure subject to random floods following a PDF fq(q), and D(qqC) is the damage function corresponding to the flood magnitude of q and hydraulic structural capacity qt. A graphic representation of Eq. (8.32) is shown in Fig. 8.10, and E1(Dx) corresponds to the shaded area under the damage-frequency curve. Owing to the complexity of the damage function and the form of the PDF of floods, the analytical integration of Eq. (8.31), in most real-life applications, is difficult, if not impossible. Hence the evaluation of annual expected damage cost by Eq. (8.32) is done numerically.

|
Note that Eq. (8.32) considers only the inherent hydrologic uncertainty owing to the random occurrence of flood events, represented by the PDF fq(q). It does not consider hydraulic and economic uncertainties. Furthermore, a perfect knowledge about the probability distribution of flood flow is assumed. This is generally not the case in reality.
Incorporation of hydraulic uncertainties. As described in Sec. 1.2, uncertainties also exist in the process of hydraulic computations for determining the flowcarrying capacity of the hydraulic structure. In other words, qc is a quantity subject to uncertainty. From the uncertainty analysis of qc (Tung and Yen, 2005), the statistical properties of qc can be estimated. Hence, to incorporate uncertainty feature of qc into the risk-based design, the annual expected damage can be calculated as
![]() f СО Г /* СО
f СО Г /* СО
E2( D) = D(qqc) fq(q)dq
in which gqc(qc) is the PDF of random flow-carrying capacity qc. Again, in practical problems, the annual expected damage estimated by Eq. (8.33) would have to evaluated through the use of appropriate numerical integration schemes.
Considering hydrologic inherent and parameter uncertainties. Since the occurrence of streamflow is random by nature, the statistical properties such as the mean, standard deviation, and skewness coefficient of the distribution calculated from a finite sample are also subject to sampling errors. In hydrologic frequency analysis, a commonly used frequency equation (Eq. 3.5) for determining the magnitude of a hydrologic event, say, a flood, of a specified return period T years is
qT = Mq + Kt Oq (8.34)
in which qT is the magnitude of the hydrologic event of the T year, Mq and oq are the population mean and standard deviation of floods, respectively, and Kt is the frequency factor depending on the skewness coefficient and distribution of the flood event.
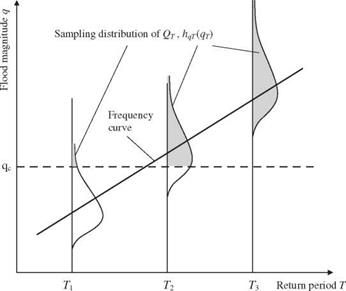
Consider floods being the hydrologic event that could potentially cause the failure of the hydraulic structure. Owing to the uncertainty associated with the estimated values of Mq, oq, and Kt in Eq. (8.34), the flood magnitude of a specified return period qT is also a random variable associated with its probability distribution (see Fig. 8.11) instead of being a single-valued quantity presented by its “average,” as commonly done in practice. Section 3.8 describes the sample distributions for some of the probability distributions frequently
|
Figure 8.11 Schematic sketch of sampling distribution of flood magnitude estimator. |
used in hydrologic flood frequency analysis. Hence there is an expected damage corresponding to the T-year flood magnitude that can be expressed as
n TO
E(Dt qC) = / D(qr q*c)hqT (qr )dqT (8.35)
■hn
where E(Dt q*) is the expected damage corresponding to a T-year flood given a known flow capacity of the hydraulic structure q*, hqT (qT) is the sampling PDF of the flood magnitude estimator of a T-year return period, and qT is the dummy variable for a T-year flood. Equation (8.35) represents an integration of flood damage over the shaded area associated with the sample distribution of a T-year flood. To combine the inherent hydrologic uncertainty, represented by the PDF of annual flood fq(q), and the hydrologic parameter uncertainty, represented by the sampling PDF for a flood sample of a given return period hqT (qT), the annual expected damage cost can be written as
![]() q
q
Incorporation of hydrologic inherent and parameter and hydraulic uncertainties. To
include hydrologic inherent and parameter uncertainties along with the hydraulic uncertainty associated with the flow-carrying capacity, the annual expected damage cost can be written as
Summary. Based on the preceding formulations for computing annual expected damage in risk-based design of hydraulic structures, one realizes that the mathematical complexity increases as more uncertainties are considered. However, to obtain an accurate estimation of annual expected damage associated with the structural failure would require the consideration of all uncertainties, if such can be practically accomplished. Otherwise, the annual expected damage would, in most cases, be underestimated, leading to inaccurate optimal design. In an application to flood levee design (Tung, 1987), numerical investigations indicate that without providing a full account of uncertainties in the analysis, the resulting annual expected damage is significantly underestimated, even with a 75-year-long flood record.







Leave a reply