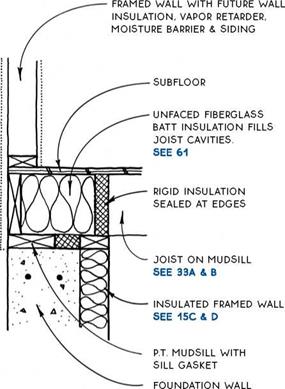
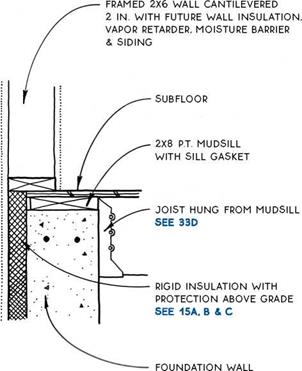
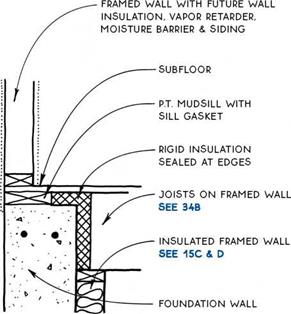
The normal distribution has been playing an important role in the development of statistical theories. This subsection briefly describes two distributions related to the functions of normal random variables.

|
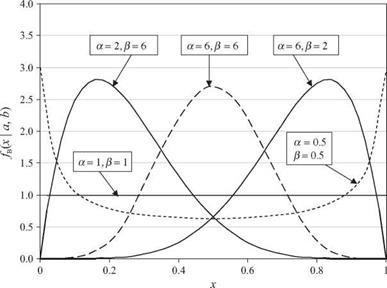
Figure 2.23 Shapes of standard beta probability density functions. (After Johnson and Kotz, 1972.)
|
|
X2 (chi-square) distribution. The sum of the squares of K independent standard normal random variables results in a x2 (chi-square) random variable with K degrees of freedom, denoted as x2- In other words,
E z2 ~ xK (2-101)
k=і
in which the Zks are independent standard normal random variables. The PDF of a x 2 random variable with K degrees of freedom is
f x2(* I K) = 2k/2r1 K/2)x(K/2-1)e-x/2 for x > 0 (2.102)
Comparing Eq. (2.102) with Eq. (2...
read more