his book is your ticket to smooth sailing when it comes to doing the math for plumbing and pipe fitting. Most of the work is already done for you when you consult the many tables and references contained in these pages. Why waste time with calculators and complicated mathematical equations when you can turn to the ready-reference tables here and have the answers at your fingertips? There is no reason to take the difficult path when you can put your field skills to better use and make more money.
A few words of advice are needed here. Our country uses multiple plumbing codes. Every code jurisdiction can adopt a particular code and amend it to their local needs. It is impossible to provide one code source to serve every plumber’s needs. The code tables in this book are meant to be used as representative samples of how to arrive at your local requirements, but they are not a substitution for your regional code book. Always consult your local code before installing plumbing.
The major codes at this time are the International Plumbing Code and the Uniform Plumbing Code. Both are excellent codes. There have been many code developments in recent years. In addition to these two major codes, there are smaller codes in place that are still active. I want to stress that this is not a handbook to the plumbing code,- this is a calculations manual. If you are interested in a pure code interpretation, you can review one of my other McGraw-Hill books entitled: International and Uniform Plumbing Codes Handbook.
re you a plumber or pipe fitter who dislikes doing the math that is required in your trade? If so, this book may be one of the best tools that you can put in your truck or office. Why? Because it does much of the math calculations for you. That’s right, the tables and visual graphics between these pages can make your life much easier and more profitable.
R. Dodge Woodson, the author, is a 30-year veteran of the trade who has been in business for himself since 1979. He knows what it takes to win in all financial climates as both a business owner and tradesman. This is your chance to learn from an experienced master plumber and, what is even better, you don’t have to study and memorize formulas. All you have to do is turn to the section of this professional reference guide that affects your work and see the answers to your questions in black and white. How much easier could it be?
Mathematical matters are not the only treasures to be found here. You will find advice on how to comply with the plumbing code quickly, easily, and without as much thought on your part.
The backbone of this book is math for the trades, but there is much more. There is a section on troubleshooting that is sure to save you time, frustration, and money. Find out what you may need to know about septic systems. In addition to phase-specific math solutions, there is an appendix that is full of reference and conversion tables for day-to-day work situations.
Take a moment to scan the table of contents. You will see that the presentation of material here is compiled in logical, accessible, easy-to-use chapters. Flip through the pages and notice the tip boxes and visual nature of the information offered. You don’t have to read much, but you will find answers to your questions.
If you are looking for a fast, easy, profitable way to avoid the dense reading and complicated math that is needed in your trade, you have found it. Once you put this ready reference guide at your fingertips, you will be able to concentrate on what you do best without the obstacles that may steal your time and your patience. Packed with 30 years of experience, you can’t go wrong by using Woodson’s resources to make you a better tradesman.
ix
This page intentionally left blank.
ath is not always a welcome topic among tradespeople. As much as math may be disliked, it plays a vital role in the trades, and plumbing and pipe fitting are no exceptions. In fact, the math requirements for some plumbing situations can be quite complicated. When people think of plumbers, few thoughts of scholarly types come to mind. I expect that most people would have trouble envisioning a plumber sitting at a drafting table and performing a variety of mathematical functions involving geometry, algebra, and related math skills. Yet, plumbers do use high-tech math in their trade, sometimes without realizing what they are doing.
 Think about your last week at work. Did you work with degrees of angles? Of course you did. Every pipe fitting you installed was an example of angles. Did you grade your drainage pipe? Sure you did, and you used fractions to do it. The chances are good that you did a lot more math than you realized. But, can you find the volume of a water heater if the tank is not marked for capacity? How much water would it take to fill up a 4-inch pipe that is 100 feet long? You might need to know if you are hauling the water in for an inspection test of the pipe. How much math you use on a daily basis is hard to predict. Much of the answer would depend on the type of work you do within the trade. But, it’s safe to say that you do use math on a daily basis.
Think about your last week at work. Did you work with degrees of angles? Of course you did. Every pipe fitting you installed was an example of angles. Did you grade your drainage pipe? Sure you did, and you used fractions to do it. The chances are good that you did a lot more math than you realized. But, can you find the volume of a water heater if the tank is not marked for capacity? How much water would it take to fill up a 4-inch pipe that is 100 feet long? You might need to know if you are hauling the water in for an inspection test of the pipe. How much math you use on a daily basis is hard to predict. Much of the answer would depend on the type of work you do within the trade. But, it’s safe to say that you do use math on a daily basis.
I’ve taught a number of classes for plumbers and plumbing apprentices. Math is usually the least appreciated part of those classes. Experience has showed me that students resist the idea of learning math skills.
I remember when I took academic levels of math in school and thought that I’d never use it. Little did I know back then how valuable the skills I was learning would be.
1
|
A or a
|
Area, acre
|
|
AWG
|
American Wire Gauge
|
|
В or b
|
Breadth
|
|
bbl
|
Barrels
|
|
bhp
|
Brake horsepower
|
|
BM
|
Board measure
|
|
Btu
|
British thermal units
|
|
BWG
|
Birmingham Wire Gauge
|
|
В & S
|
Brown and Sharpe Wire Gauge (American Wire Gauge
|
|
C of g
|
Center of gravity
|
|
cond
|
Condensing
|
|
cu
|
Cubic
|
|
cyl
|
Cylinder
|
|
D or d
|
Depth, diameter
|
|
dr
|
Dram
|
|
evap
|
Evaporation
|
|
F
|
Coefficient of friction; Fahrenheit
|
|
F or f
|
Force, factor of safety
|
|
ft (or ‘I
|
Foot
|
|
ft lb
|
Foot pound
|
|
fur
|
Furlong
|
|
gal
|
Gallon
|
|
gi
|
Gill
|
|
ha
|
Hectare
|
|
H or h
|
Height, head of water
|
|
HP
|
horsepower
|
|
IHP
|
Indicated horsepower
|
|
in for ")
|
Inch
|
|
L or l
|
Length
|
|
lb
|
Pound
|
|
lb/sq in.
|
Pounds per square inch
|
|
mi
|
Mile
|
|
o. d.
|
Outside diameter (pipes)
|
|
oz
|
Ounces
|
|
pt
|
Pint
|
|
P or p
|
Pressure, load
|
|
psi
|
Pounds per square inch
|
|
R or r
|
Radius
|
|
rpm
|
Revolutions per minute
|
|
sq ft
|
Square foot
|
|
sq in.
|
Square inch
|
|
sq yd
|
Square yard
|
|
T or t
|
Thickness, temperature
|
|
temp
|
Temperature
|
|
V or v
|
Velocity
|
|
vol
|
Volume
|
|
W or w
|
Weight
|
|
W. I.
|
Wrought iron
|
FIGURE 1.1 ■ Abbreviations. (Courtesy of McGraw-Hill)
While I’m not a rocket scientist, I can take care of myself when it comes to doing math for trade applications.
I assume that your time is valuable and that you are not interested in a college course in mathematics by the end of this chapter. We’re on the same page of the playbook. I’m going to give you concise directions for solving mathematical problems that are related to plumbing and pipefitting. We won’t be doing an in-depth study of the history of numbers, or anything like that. The work we do here will not be too difficult, but it will prepare you for the hurdles that you may have to clear as a thinking plumber. So, let’s do it.
The quicker we start, the quicker we can finish.
BENCHMARKS
Before we get into formulas and exercises, we need to establish some benchmarks for what we will be doing. It always helps to understand the terminology being used in any given situation, so refer to Figure 1.1 for reference to words and terms being used as we move forward in this chapter. The information in Figure 1.2 shows you some basic formulas that can be applied
FIGURE 1.2 ■ Useful formulas. (Courtesy of McGraw-Hill)
FIGURE 1.3 ■ Trigonometry. (Courtesy of McGraw-Hill)

 to many mathematical situations. Trigonometry is a form of math that can send some people in the opposite direction. Don’t run, it’s not that bad. Figure 1.3 provides you with some basics for trigonometry, and Figure 1.4 describes the names of shapes that contain a variety of sides. Some more useful formulas are provided for you in Figure 1.5. Just in what I’ve provided here, you are in a much better position to solve mathematical problems. But, you probably want, or need, a little more explanation of how to use your newfound resources. Well, let’s do some math and see what happens.
to many mathematical situations. Trigonometry is a form of math that can send some people in the opposite direction. Don’t run, it’s not that bad. Figure 1.3 provides you with some basics for trigonometry, and Figure 1.4 describes the names of shapes that contain a variety of sides. Some more useful formulas are provided for you in Figure 1.5. Just in what I’ve provided here, you are in a much better position to solve mathematical problems. But, you probably want, or need, a little more explanation of how to use your newfound resources. Well, let’s do some math and see what happens.

|
Pentagon 5 sides
Hexagon 6 sides
Heptagon 7 sides
Octagon 8 sides
Nonagon 9 sides
Decagon 10 sides
|
|
FIGURE 1.4 ■ Polygons. (Courtesy of McGraw-Hill)
|
Parallelogram
Pyramid
Rectangle Rectangular prism Sphere
Square
Triangle
Trapezoid
Cone
|
|
|
Area = base x distance between the two parallel sides
Area = ‘h perimeter of base x slant height + area of base
Volume = area of base x l/> of the altitude
Area = length X width
Volume = width x height x length
Area of surface = diameter x diameter X 3.1416
Side of inscribed cube = radius x 1.547
Volume = diameter x diameter x diameter X 0.5236
Area = length x width
Area = one-half of height times base
Area = one-half of the sum of the parallel sides x the height
Area of surface = one-half of circumference of base X slant height + area of base
Volume = diameter x diameter x 0.7854 x one-third of the altitude
|
|
|
|
|
Volume = width X height X length
Area = short diameter x long diameter x 0.7854
Area of surface = diameter x 3.1416 X length + area of the two bases
Area of base = diameter x diameter x 0.7854
Area of base = volume – e length
Length = volume – e area of base
Volume = length x area of base
Capacity in gallons = volume in inches + 231
Capacity of gallons = diameter x diameter x length x 0.0034
Capacity in gallons = volume in feet x 7.48 Circumference = diameter X 3.1416 Circumference = radius x 6.2832 Diameter = radius x 2
Diameter = square root of = (area – e 0.7854)
Diameter = square root of area x 1,1233
|
|
|
|






 time consuming, there is still no guarantee that there will be enough room for the grade. Knowing how to figure the grade, fall, pitch, or whatever you want to call it, for a pipe is essential in the plumbing trade. And, it’s not difficult. Let me show you what I mean.
time consuming, there is still no guarantee that there will be enough room for the grade. Knowing how to figure the grade, fall, pitch, or whatever you want to call it, for a pipe is essential in the plumbing trade. And, it’s not difficult. Let me show you what I mean.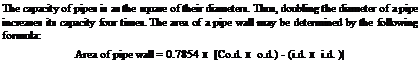

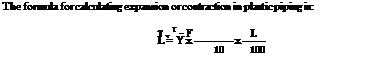
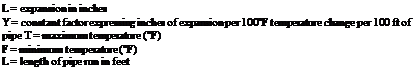

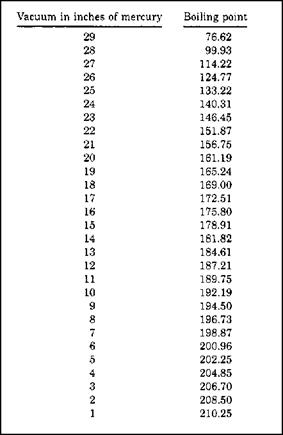

 Think about your last week at work. Did you work with degrees of angles? Of course you did. Every pipe fitting you installed was an example of angles. Did you grade your drainage pipe? Sure you did, and you used fractions to do it. The chances are good that you did a lot more math than you realized. But, can you find the volume of a water heater if the tank is not marked for capacity? How much water would it take to fill up a 4-inch pipe that is 100 feet long? You might need to know if you are hauling the water in for an inspection test of the pipe. How much math you use on a daily basis is hard to predict. Much of the answer would depend on the type of work you do within the trade. But, it’s safe to say that you do use math on a daily basis.
Think about your last week at work. Did you work with degrees of angles? Of course you did. Every pipe fitting you installed was an example of angles. Did you grade your drainage pipe? Sure you did, and you used fractions to do it. The chances are good that you did a lot more math than you realized. But, can you find the volume of a water heater if the tank is not marked for capacity? How much water would it take to fill up a 4-inch pipe that is 100 feet long? You might need to know if you are hauling the water in for an inspection test of the pipe. How much math you use on a daily basis is hard to predict. Much of the answer would depend on the type of work you do within the trade. But, it’s safe to say that you do use math on a daily basis.

 to many mathematical situations. Trigonometry is a form of math that can send some people in the opposite direction. Don’t run, it’s not that bad. Figure 1.3 provides you with some basics for trigonometry, and Figure 1.4 describes the names of shapes that contain a variety of sides. Some more useful formulas are provided for you in Figure 1.5. Just in what I’ve provided here, you are in a much better position to solve mathematical problems. But, you probably want, or need, a little more explanation of how to use your newfound resources. Well, let’s do some math and see what happens.
to many mathematical situations. Trigonometry is a form of math that can send some people in the opposite direction. Don’t run, it’s not that bad. Figure 1.3 provides you with some basics for trigonometry, and Figure 1.4 describes the names of shapes that contain a variety of sides. Some more useful formulas are provided for you in Figure 1.5. Just in what I’ve provided here, you are in a much better position to solve mathematical problems. But, you probably want, or need, a little more explanation of how to use your newfound resources. Well, let’s do some math and see what happens.