PIPING MATH
This section will profile formulas that can help you when working with pipes. Rather than talk about them, let’s look at them.
What plumber hasn’t had to figure the grading for a drainage pipe? Determining the amount of fall needed for a drainpipe over a specified distance is no big mystery. Yet, I’ve known good plumbers who had trouble with calculating the grade of their pipes. In fact, some of them were so unsure of themselves that they started at the end of their runs and worked backwards, to the beginning, to insure enough grade. Not only is this more difficult and
 time consuming, there is still no guarantee that there will be enough room for the grade. Knowing how to figure the grade, fall, pitch, or whatever you want to call it, for a pipe is essential in the plumbing trade. And, it’s not difficult. Let me show you what I mean.
time consuming, there is still no guarantee that there will be enough room for the grade. Knowing how to figure the grade, fall, pitch, or whatever you want to call it, for a pipe is essential in the plumbing trade. And, it’s not difficult. Let me show you what I mean.
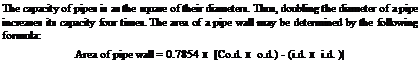 |
In a simple way of putting it, assume that you are installing a pipe that is 20 feet long and that will have a grade of V4-inch per foot. What will the drop from the top of the pipe be from one end to the other? At a grade of V-t-inch per foot, the pipe will drop one inch for every four feet it travels. A 20-foot piece of pipe will require a 5- inch drop in the scenario described. By dividing 4 into 20, I got an answer of 5, which is the number of inches of drop. That’s my simple way of doing it,
 |
FIGURE 1.6 ■ Piping. (Courtesy of McGraw-Hill)
FIGURE 1.7 ■ Determining pipe weight. (Courtesy of McGraw-Hill)
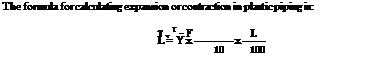 |
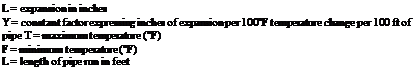 |
FIGURE 1.8 ■ Expansion in plastic piping. (Courtesy of McGraw-Hill)
|
The formulas for pipe radiation of heat are as follows:
D = outside diameter (OD) of pipe L = length of pipe needed in feet R = square feet of radiation needed |
FIGURE 1.9 ■ Formulas for pipe radiation of heat. (Courtesy of McGraw-Hill)
but now let me give you the more proper way of doing it with a more sophisticated formula.
If you are going to use the math formula, you must know the terms associated with it. Run is the horizontal distance that the pipe you are working with will cover, and this measurement is shown as the letter R. Grade is the slope of the pipe and is figured in inches per foot. To define grade in a formula, the letter G is used. Drop is the amount down from level or in more plumber-friendly words, it’s the difference in height from one end of the pipe to the other. As you might guess, drop is known by the letter D. Now let’s put this into a formula. To determine grade with the formula above, you would be looking at something like this: D = G X R. If you know some of the variables, you can find the rest. For example, if you know how far the pipe has to run and what the maximum amount of drop can be, you can determine the grade. When you know the grade and the length of the run, you can determine the drop. I already showed you how to find the drop if you know grade and run numbers. So, let’s assume an example where you know that the drop is 15 inches and the run is 60 feet, what is the grade? To find the answer, you divide the drop by the run, in this case you are dividing 15 by 60. The answer is.25 or V4-inch per foot of grade.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-100°-30° |
||
|
QC |
Base temperature |
|
|
-73 |
-100 |
-148 |
|
-68 |
-90 |
-130 |
|
-62 |
-80 |
-112 |
|
-57 |
-70 |
-94 |
|
-51 |
-60 |
-76 |
|
-46 |
-50 |
-58 |
|
-40 |
-40 |
-40 |
|
-34.4 |
-30 |
-22 |
|
-28.9 |
-20 |
-4 |
|
-23.3 |
-10 |
14 |
|
-17.8 |
0 |
32 |
|
-17.2 |
1 |
33.8 |
|
-16.7 |
2 |
35.6 |
|
-16.1 |
3 |
37.4 |
|
-15.6 |
4 |
39.2 |
|
-15.0 |
5 |
41.0 |
|
-14.4 |
6 |
42.8 |
|
-13.9 |
7 |
44.6 |
|
-13.3 |
8 |
46.4 |
|
-12.8 |
9 |
48.2 |
|
-12.2 |
10 |
50.0 |
|
-11.7 |
11 |
51.8 |
|
-11.1 |
12 |
53.6 |
|
-10.6 |
13 |
55.4 |
|
-10.0 |
14 |
57.2 |
|
ЗГ-7Г |
||
|
°С |
Base temperature |
°F |
|
-0.6 |
31 |
87.8 |
|
0 |
32 |
89.6 |
|
0.6 |
33 |
91.4 |
|
1.1 |
34 |
93.2 |
|
1.7 |
35 |
95.0 |
|
2.2 |
36 |
96.8 |
|
2.8 |
37 |
98.6 |
|
3.3 |
38 |
100.4 |
|
3.9 |
39 |
102.2 |
|
4.4 |
40 |
104.0 |
|
5.0 |
41 |
105.8 |
|
5.6 |
42 |
107.6 |
|
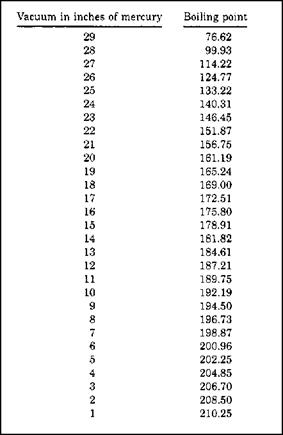
FIGURE 1.14 ■ Boiling points of water based on pressure. (Courtesy of McGraw-Hill) |






Leave a reply