Water in the Vadose Zone
The groundwater table is defined as the locus of points at atmospheric pressure. Below the water table the pore water pressure is positive and in a hydrostatic state, while the pore water pressure increases linearly with depth. Above the groundwater table, in the vadose zone, water only remains in the pores due to capillary action. The water pressure is then negative or less than the atmospheric pressure and capillary pressures, known as matric suctions, exist. Large matric suctions correspond to large negative water phase pressures and soils under such conditions usually have low water saturations. Furthermore, both the water content and therefore the permeability are nonlinear functions of these capillary conditions.
In unsaturated soils, pore spaces are filled with both water and air. The water is held in the soil pores by surface tension forces. These lead to a pressure difference between the air and water in the porous medium, as long as the interface is curved. As the curvature of the interface between the two phases – the air and the water – changes with the amount of water (or moisture content) in the soil, the matric suction is dependent on the water content. This relationship is non-linear, greatly complicating analyses of water flow through unsaturated soils.
The capillary conditions are described by the matric suction, 5 (expressed in pressure terms) or can be described in terms of the matric potential, Ф, which represents the height (head) of a column of water that could be induced by such a suction. Although negative with respect to zero (i. e. atmospheric pressure), Ф and 5 are usually expressed as positive quantities and are simply related as follows:
 у
у
V = (2.26)
Pw g
where pw is the density of water and g is the acceleration due to gravity. Matric suction is related to the phase pressures and interface curvature by the relationship:
2оі
s = ua — u = – (2.27)
Гс
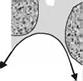
where ua and u are the air and water pressures, respectively, ai is the interfacial energy or the surface tension and rc is the average radii of curvature as illustrated in Fig. 2.8.
In the unsaturated zone, because part of the soil pores are filled with water while the rest is filled with air, therefore the sum of the volumetric water, в, and air, 9a, contents must be equal to the total porosity, n:
![]() в + в a = П
в + в a = П
This equation may also be written in terms of water saturation, Sr, that is
Sr + Sa = 1 (2.29)
where Sa is the air saturation content.
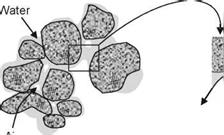
To understand the distribution of water in the unsaturated soils we may consider a soil mass that is initially dry. Upon addition of water, the water is first adsorbed as film on the surface of the soils grains. This thin skin of adsorbed water is usually called pellicular water (Bear, 1972) and is held strongly by van der Waal’s forces and can hold very high matric suctions. Thus even if a matric suction of tens of atmospheres were applied this water would not be removed from the soil.
If water is further added, water starts to accumulate at the contact point between the grains that represent the smallest pore space openings. This water is referred to as the pendular water. The pendular water is held at the contact points by capillary forces. Capillary forces are caused by the presence of surface tension between the air and the water phases within the soil voids and causes water to move into the
Fig. 2.8 (a) Distribution of water in a porous media. (b) Curved interface separating water and air phases
smallest pores. At this stage water movement through the soil skeleton is slow even under large hydraulic gradients because the water is forced to move along the thin film of adsorbed water. As the water content increases the film get thicker and water moves more easily.
As the water content continues to increase the water saturation reaches the stage where air becomes isolated in individual pockets in the larger pores and flow of air is no longer possible. This saturation is called insular saturation. These air pockets may dissolve leading to full water saturation of the soil.






Leave a reply