Permeability Tests of Unsaturated Soils

As introduced in Chapter 2, the flow of water in saturated soils is commonly de­scribed using Darcy’s law which relates the rate of water flow to the hydraulic gra­dient (Eq. 2.16). Furthermore the coefficient of permeability is relatively constant for a specific soil. Darcy’s law applies also to the flow of water through unsaturated soils. However the permeability of unsaturated soils can not be assumed generally to be constant (Richards, 1931; Fredlund & Rahardjo, 1993; Fredlund 1997). Per­meability now becomes predominantly a function of either the water content or the matric suction (see Chapter 2, Section 2.8). The main reason for this is linked to the fact that the pores in the material are the channels through which the wa­ter flows. In saturated soils all pores are filled with water, allowing the water to move. In unsaturated soils however not all the pores are filled with water. The air-filled pores are therefore not active in transporting water through the material. They can therefore be assumed to behave in a similar way as the solid phase. The permeability of unsaturated soils is therefore lower than in the same soil in a saturated state and decreases as the water content decreases or matric suction increases.

A number of methods exist to measure the unsaturated permeability of soils, both in the laboratory and in the field. As for saturated methods, they can be classified into steady or unsteady methods. In the laboratory the steady state method is rec­ommended as it is relatively simple and has few ambiguities. However the method can be quite time consuming as the flow rate can be very low, especially under conditions of high matric suction. Further it can be difficult to measure the low flow rate accurately due to air diffusion. More recently a faster steady state method has been introduced where a centrifuge is introduced to drive the fluid flow (Nimmo et al., 1987; 1992). The unsteady laboratory methods, such as the thermal method, instantaneous profile method and the multi-step outflow method are usually much quicker than the traditional steady state method but are usually not as accurate. In the field the tension infiltrometer, instantaneous profile method and the cone penetrom­eter methods can be used. Benson & Gribb (1997) give a comprehensive overview of methods to measure the permeability of unsaturated soils.

The coefficient of permeability of unsaturated soils is not routinely measured in the laboratory as the process is cumbersome and quite time consuming (Fredlund 2006). The permeability of unsaturated soils can also be indirectly estimated from the SWCC. This is attractive as the SWCC can be determined in a much shorter time than the permeability’s dependency on matric suction and with greater reliability (Rahardjo & Leong, 1997).

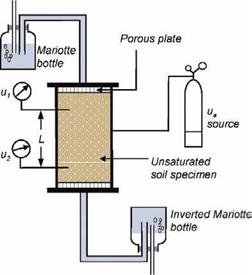In the steady state method, the unsaturated permeability is measured under con­ditions of a constant matric suction. A constant hydraulic head gradient is applied over an unsaturated soil sample with a constant matric suction to produce a steady state water flow through the specimen (see Fig. 3.11). A Mariotte bottle can be used to provide a constant pore water pressure to deliver a constant rate of flow. When the rates of water flow entering and leaving the sample are equal, the steady state has been reached and the coefficient of the permeability can be calculated according to Darcy’s law (Eq. 2.15) as

h u і — u2

v = — K — = K— 2 (3.14)

L pwgL

where v is the flow rate of water through the sample, K is the coefficient of perme­ability and h/L is the hydraulic head gradient across the sample (with h the head difference and L the length of the sample). The head difference can be estimated from ui and u2, the readings from the two pore water pressure sensors, converting pressure to head by dividing by the density of water, pw and the acceleration due to gravity, g.

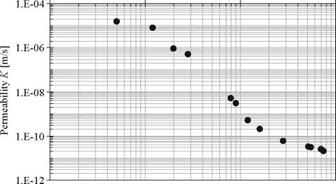
Now the test is repeated for different suctions in order to establish the relationship between the permeability and the suction. A typical measurement of permeability as a function of the matric suction is given in Fig. 3.12. As matric suction is related to water content through the SWCC, and if that relationship is known, the variation of permeability with water content is also known. Notice that, for the suction range illustrated, the coefficient of permeability changes by 6 orders of magnitude.