Darcy’s Law
Water flows though porous media from a point to which a given amount of energy can be associated to another point at which the energy will be lower (Cedergren, 1974, 1977). The energy involved is the kinetic energy plus the potential energy. The kinetic energy depends on the fluid velocity but the potential energy is linked to the datum as well as the fluid pressure. As the water flows between the two points a certain head loss takes place.
From an experimental setup as shown in Fig. 2.6, the total energy of the system between points A and B is given from Bernoulli equation as
![]() UA V A uB vB
UA V A uB vB
— + TT + ZA = — + ^ + ZB + Ah Pwg 2g Pwg 2g
where u and v are the fluid pressure and velocity respectively, z is elevation above the datum line and h is head loss between point A and B that is generating the flow. As velocities are very small in porous media, velocity heads may be neglected, allowing head loss to be expressed as:
h = ^ + zA -( + zb) (2.14)
Pw g Pw g J
Darcy related flow rate to head loss per unit length through a proportion constant referred to as K, the coefficient of permeability (also known as the coefficient of hydraulic conductivity) as:
![]() VK
VK
P. S
![]() p. g
p. g
B
Datum
Fig. 2.6 Head loss as water flows through a porous media. Where u = pore water pressures, h = heads, z & L = distances
or in more general terms, at an infinitesimal scale:
dh
v = -K = – Ki (2.16)
dl
where dh is the infinitesimal change in head over an infinitesimal distance, dl, and i is the hydraulic gradient of the flow in the flow direction. The above equation is known as Darcy’s law and governs the flow of water through soils (see Eq. 1.2).
It should be pointed out that Darcy’s law applies to laminar, irrotational flow of water in porous media. For saturated flow the coefficient of permeability may be treated as constant provided eddy losses are not significant (see below). Above the groundwater table, in the unsaturated zone, Darcy’s law is still valid but the permeability will be a function of the water content, thus K = K(9w), as described in Section 2.8.
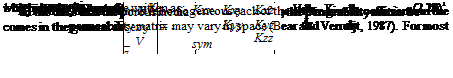
Darcy’s law can easily be extended to two or three dimensions. For three dimensions using a Cartesian coordinate system Darcy’s law is given for a homogeneous isotropic medium as
highway engineering problems the porous media, that is each layer, can be assumed homogenous and isotropic.
For very coarse grained soils or aggregates, some of the voids in the material become quite large and the assumption of a laminar flow of water is no longer valid. Instead of irrotational flow, eddy currents develop in the larger voids and/or the flow may become turbulent involving more energy loss than in a laminar flow. For these circumstances the hydraulic gradient in Darcy’s law can be replaced with Forcheimer’s law:
![]() , V V2
, V V2
– = K + K
where two coefficient of permeability, K1 [LT-1] and K2 [L2T-2], are now required to describe the behaviour.
In highway practice this means that coarse aggregates with large pores – such as those which comprise typical granular base courses – must be tested at low hydraulic gradients to ensure laminar flow is maintained and that appropriate values of K are obtained. This aspect is covered further in Chapter 3, Section 3.3.1 (see Fig. 3.7 in particular).






Leave a reply