The hydraulic works of Greece during the classical era do not measure up to those of the Mycenaen era. The few extracts cited above also show that in Greece, hydraulic know-how lags behind that of the Orient. And yet this classical Greece is known to us as the privileged cradle of development of philosophical and mathematical thought. Two facts are important in this regard. First, Greek science at this period took it as a point of honor to be disconnected from engineering, i. e. not to be associated with practical applications. Second, and it is here that one can effectively and for perhaps the first time refer to science, the “sages” sought to apply reasoning to the explanation of great natural phenomena.
Such explanations of natural phenomena are often incomplete, and sometimes false. Regarding the hydrologic cycle, the brilliant mathematician and astronomer Thales of Miletus (610 — 545 BC?) — who had established that the world is round — postulated that water is the primordial substance and that the land masses float upon it. This is a theory perhaps inspired by the ancient Mesopotamian and Egyptian cosmologists. Later, Anaximandre of Miletus (610 — 545 BC) identifies the origin of precipitation as water torn from the earth’s surface by solar action. Xenophane of Colophon (570 — 475 BC?) writes that the sea, source of all water, is also the origin of clouds and winds, that fresh water comes from evaporation of the sea, that rivers result from rain, and that it is by rinsing the ground that watercourses carry salt to the sea. The hydrologic cycle is therefore fairly well understood in Greek civilization of the 6th century BC, except for the role of groundwater. Indeed, during this period it was thought that the water in springs and wells comes from the sea.
Plato (427 — 347 BC?) adopts the idea, articulated before him by Empedocle of Agrigente, of the four primordial elements: water, air, fire, and earth. His student Aristotle (385 — 322 BC), born in Macedonia, frequents Plato’s Academy until the death of the master, and becomes preceptor of Alexander at the court of Philippe of
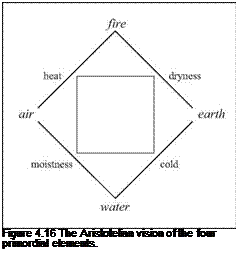Macedonia. At Athens he creates the institution called the Lyceum. Aristotle in his turn adopts the theory of the four elements, a theory that will remain a standard reference until the Middle Ages. He believed that each of these elements tends to return to its natural place, e. g. water below the ground, air above water, etc. Thus, for Aristotle, wood floats because it contains air, and it is in the natural order of things that air be above water. To each element is attributed two of the four fundamental “qualities”: cold, moistness, heat, and dryness (Figure 4.16).
Attempts to explain nature from such a postulate can obviously lead to absurd conclusions. Here is how Aristotle, reflecting his ignorance of what we now call inertia, shows in his Physics that a vacuum cannot exist, and in so doing sets down an absurd theory of wind resistance. First, in virtue of the natural “position” of each element, as we have seen above, if an object (for example a stone thrown by a man) moves through the air, “outside” of its natural position, there is an action, a “motor” that sustains its movement:
. .earth and all other bodies should remain in their proper places and be moved from them only by violence. J
Then, since “it seems that everything in motion is impelled by something”, the stone that continues its movement through the air must be sustained, in its movement, by the air itself:
”(…) things that are thrown move (although that which gave them their impulse is not touching them, either by reason of mutual replacement, as some maintain, or because the air that has been pushed pushes them with a movement quicker than the natural locomotion of the projectile wherewith it moves to its proper place.”[161] [162]
Aristotle continues his demonstration in postulating that in a vacuum, all movement would be impossible — i. e. in the absence of this air that “maintains” movement. Therefore “there is no vacuum separate from things”.
At about this same time Pytheas (380 — ? BC), of the Phoenician colony of Massalia (Marseilles), sets out on a voyage that leads him to the great north, probably as far as Iceland. During this voyage he establishes a correlation between the periodic phenomenon of the tides and lunar cycles.
Overall, one can only admire this quest for truth as representing progress and promise for the future. Yet it is also clear that during the Greek classical era, hydraulic theories are, at best, rudimentary. It is not until the Hellenistic period and the intellectual movement coming out of the school of Alexandria that mathematics and the faculty of reasoning lead to practical innovation.
