Archimedes, and the first theoretical formulations of fluid mechanics
Archimedes (287 – 212 BC) was born at Syracuse, in Sicily. In all probability, he spent time in Alexandria where he studied geometry with the followers of Euclid. Though Archimedes belonged to the mathematical School, it would have been quite natural and possible for him to see the inventions of Ctesibios during his stay. Upon his return to Syracuse, he continued to correspond with the scholars of Alexandria, in particular with the mathematician Conon of Samos, and with the director of the Library, Eratosthene.11 This justifies the association of Archimedes’ work with the school of Alexandria.
First and foremost a mathematician, Archimedes was interested in the problem of buoyancy of bodies of arbitrary shape. Extreme rigor distinguishes his work – he first proposes axioms, then demonstrates their consequences. The initial postulate of his work on “floating bodies” introduces the notion of pressure:
“We take as a principle that liquid is of such a nature that, its parts being arranged in an equal and contiguous manner, the part that is the least compressed is displaced from its position by
|
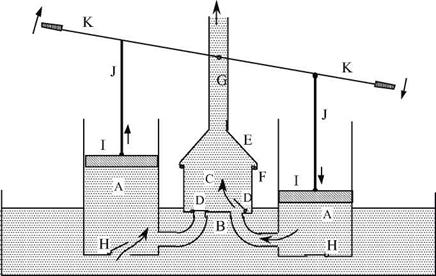
Figure 5.5 The two-body pump of Ctesibios of Alexandria, as it is described by Vitruvius: “It is appropriate now to describe the machine of Ctesibios, which lifts water. This machine must be made of bronze. At its base, and quite near to each other, are twin cylinders (A), to which are connected tubes which, forming a fork (B), converge symmetrically to an intermediate chamber (C). In this chamber are two flaps (D), precisely adjusted to cover the upper openings of the tubes; blocking the openings of these orifices, they prevent the return of fluid that air (itis notair, but the waterpressure!) has driven from the chamber. Above this chamber is a cover in the shape of an inverted funnel (E) that is held down by a slotted key to resist the raising effect of the water pressure. Another tube, called a trump, is vertically mounted above the cover. Under the lower openings of the tubes, the cylinders have additional flaps (H) covering openings in their bases. The pistons (I), nested in the upper portions of the cylinders, smoothed and lubricated with oil, are activated by rods (J) and levers (K); [….] thus, from a reservoir at a low location, water can be made to gush forth.”12 |
a more compressed part, and that each of these parts is compressed by the liquid above it,
I 3
unless the liquid is in a closed receptacle and is compressed by something else.”
As early as on the second page of his treatise, he reaches a remarkable conclusion – the surface of water at rest is not horizontal, but spherical:
“The surface of any liquid at rest will have the form of a sphere having the same center as that of the earth.”[174] [175] [176]
Later on, the pragmatic Roman engineers were perplexed by this proposition: was it
|
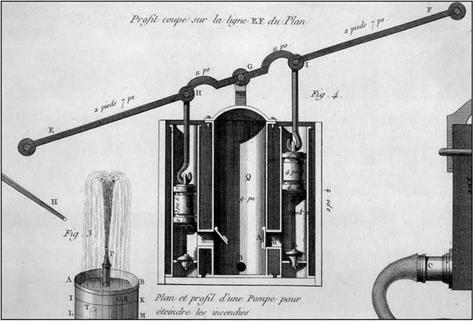
Figure 5.6 A variation of the pump of Ctesibios: a fire pump from the 18th century (Belidor, 1737) ancient archives of ENPC |
then not possible to rely on a water surface to represent a horizontal plane?[177]
Further on in this same treatise, laid out with the same rigor, are the various propositions that comprise the theory of floating bodies and the well-known formulation of Archimedes’ Principle:
“Solid objects which have (for the same volume) the same weight as the liquid in which they are immersed, when released remain submerged in such a way as not to rise to the surface of the liquid or descend further down within it.
“Any solid object lighter than a liquid (for the same volume), released in this liquid, will be submerged to a level such that the liquid which occupies the volume of the submerged portion has the same weight as the entire solid body.
“Solid bodies lighter than a liquid (for the same volume), plunged into the liquid by force, are pushed upwards by a force equal to the excess of the weight of the body over the weight of the liquid which occupies the same volume as the solid body.
“Bodies heavier than a liquid (for the same volume), released in the liquid, descend toward the bottom until reaching it, and they are lightened in the liquid by the weight of the liquid contained in a volume equal to that of the solid body.
“If a body lighter than a liquid (for the same volume) is released in the liquid, the ratio of its weight to the weight of the same volume of liquid will be equal to the ratio of the submerged part to the total.”
In his treatise, Archimedes then determines the equilibrium of diverse solids in the form of spheres, hyperboloids of revolution, etc.






Leave a reply