Triangle perimeters are not difficult to establish. The process is similar to the one used with squares, only there is one less measurement. To find the perimeter of a triangle, add up the sum total of the three sides of the shape. if you want a formula to use, it could look like this: P = A + B + C. The long and the short of it, no pun intended, is that you simply add up the three dimensions and you have the perimeter.
Circles
Circles can give you some trouble when you are looking for their perimeters, which should really be called their circumference. I have provided resource tables in the next chapter that will help you to avoid doing the math to find the circumference of a circle, but we should at least take a few moments to
|
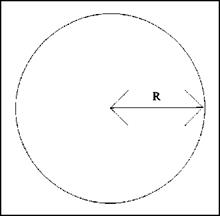
FIGURE 1.15 ■ Radius of a circle. |
|
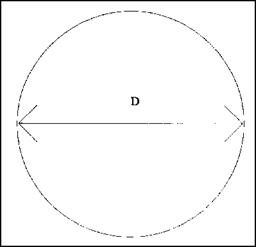
FIGURE 1.16 ■ Diameter of a circle. |
explore the procedure while we are here. Circles can be tricky, but they aren’t really all that tough. Let’s look at a couple of formulas that you shouldn’t experience problems with (Fig. 1.16).
When you want to find the circumference of a circle, you must work with the diameter (D), the radius (R), and л, which is 3.1416. You can use one of two formulas to solve your problem, depending on which variable is known. If you know the diameter, use the following formula: C = л d. When you know the radius, use this formula: C = 2лг. If the diameter is six inches, your formula would reveal that pi (3.1416) times 6 inches equals 18.8496 inches. This number would be rounded to 18.85 inches. If you knew the radius and not the diameter, your numbers would be 2 times л (3.1416) times 3 inches. The same answer would be arrived at, for a circumference of 18.85 inches. The formulas are not difficult, but using the tables in the next chapter might be faster and easier for you.
