ROOF DRAIN SIZING METHOD

B101.2 Solution:

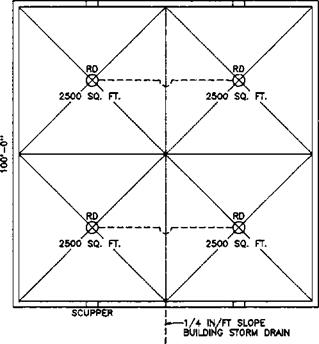
Step 1. From Fig. 6.11 the 100 year 60 minute precipitation is 3.75 inches per hour. Step 2. Each vertical drain must carry 2,500 sq ft of roof area at 3.75 inches per hour of rainfall. To convert to an area for a 4 inch per hour rainfall to enter Fig. 6.9 do this:

2.500 x 3.75 — e 4 — 2,344 sq ft. Enter Fig. 6.9 until you find a diameter pipe that will carry 2,344 sq ft. A minimum 4-inch vertical drain is required.

Step 3. Horizontal Drain 2,500 sq ft

To convert to an area for use in Fig. 6.9 do this:

2.500 X 3.75 H = 2,344 sq ft

Enter Fig. 6.9 until you find a diameter pipe that will carry 2,344 sq ft. A min­imum 4-inch diameter pipe with a ‘A inch per foot slope will carry 2,650 sq ft. A minimum 4-inch diameter drain on a V* inch per foot slope is required.

Step 4. Horizontal Drain

5.0 sq ft

To convert to an area for use in Fig. 6.9 do this:

5.0 x 3.75 — e 4 = 4,688 sq ft.

Enter Table 1108.2 until you find a diameter pipe that will carry 4,688 sq ft. A 5-inch diameter pipe with a V* inch per foot slope will carry 4,720 sq ft. A min­imum 5-inch diameter drain on a ‘A inch per foot slope is required.

Step 5. Horizontal Drain

10.0 sq ft

To convert to an area for use in Fig. 6.9 do this:

10.0 x 3.75 + 4 = 9,375 sq ft

Enter Fig. 6.9 until you find a diameter pipe that will carry 9,375 sq ft. An 8- inch diameter pipe on 1.4 inch per foot slope will carry 16,300 sq ft but a 6-inch will carry only 7,550 sq ft, therefore, use an 8-inch diameter drain on a V«inch per foot slope.

Step 6. From Fig. 6.12 the rate caused by a 100 year 15 minute precipitation is 7.2 inches per hour. The scuppers must be sized to carry the flow caused by a rain fall rate of 7.2 inches per hour.

Step 7. Each scupper is draining 2,500 sq ft of roof area. To convert this roof area to an area for use with Fig. 6.15 do this:

2.500 X 7.2 — E 4 = 4,500 sq ft

FIGURE 6.14 ■ Rainwater sizing example. (Courtesy of Standard Plumbing Code)

Enter Fig. 6.15 to find a length (see Fig. 6.15) and head that will carry 4,500 sq ft or more.

From Fig. 6.15 a 12-inch wide weir with a 4-inch head carries 6,460 sq ft.

Use 12-inch wide x 5-inch high scuppers at four locations.

A height of 5 inches is needed to assure an open area above the 4-inch head.

Step 8. Notify the structural engineer that the design of the roof structure must account for a height of water to the scupper entrance elevation plus 4 inches for the required head to cause design flow.

Note:

Table based on rainfall of 4 inches per hour.

FIGURE 6.15 ■ Scupper sizing table roof area (sq ft.). (Courtesy of Standard Plumbing Code)