Treatment of correlated normal stochastic variables

When some of the stochastic basic variables involved in the performance func­tion are correlated, transformation of correlated variables to uncorrelated ones is made. Consider that the stochastic basic variables in the performance func­tion are multivariate normal random variables with the mean matrix p, x and the covariance matrix Cx. Without losing generality, the original stochastic basic variables are standardized according to Eq. (4.30) as X’ = D—1|2(X — p, x).

Therefore, the standardized stochastic basic variables X’ have the mean 0 and covariance matrix equal to the correlation matrix Rx. That is, Cx = Rx = [pjjk], with pjk being the correlation coefficient between stochastic basic variables Xj and Xk.

To break the correlative relation among the stochastic basic variables, or­thogonal transformation techniques can be applied (see Appendix 4C). As an example, through eigenvalue-eigenvector (or spectral) decomposition, a new vector of uncorrelated stochastic basic variables U can be obtained as

U = V1X’ (4.64)

in which Vx is the normalized eigenvector matrix of the correlation matrix Rx of the original random variables. The new random variables U have a mean vector 0 and covariance matrix Lx = diag(Xb X2,…, ), which is a diagonal

matrix containing the eigenvalues of Rx. Hence the standard deviation of each uncorrelated standardized stochastic basic variable Uk is the square root of the corresponding eigenvalue, that is, VX*. Further standardization of U leads to

Y = Л — 1/2U (4.65)

in which Y are uncorrelated random variables having a mean vector 0 and covariance matrix I being an identity matrix.

Consider that the original stochastic basic variables are multivariate nor­mal random variables. The orthogonal transformation by Eq. (4.64) is a linear transformation; the resulting transformed random variables U are individu­ally normal but uncorrelated; that is, U ~ N(0, L) and Y = Z’ ~ N(0, I). Then the relationship between the original stochastic basic variables X and the uncorrelated standardized normal variables Z’ can be written as

Z’ = Л-1/2 VxD-1/2(X — »x) (4.66a)

X = vx + D1/2 V x Л1/2 Z’ (4.66b)

in which Лx and Vx are, respectively, the eigenvalue matrix and eigenvector matrix corresponding to the correlation matrix Rx.

In the transformed domain as defined by Z’, the directional derivatives of the performance function in z ‘-space can be computed, according to Eq. (4.37), as

Vz — W'(z 0 |V* W'(z 0|

in which the vector of sensitivity coefficients in Z’-space sz> = Vz W'(z’) can be obtained from VxW (x) using the chain rule of calculus, according to Eq. (4.66b), as

д X* 9 Zj

VxW (x)

Sz’ = Vz W (z’)

D1/2VxЛУ2 ) VxW(x) = ЛУ2DУ2VtSx

in which sx is the vector of sensitivity coefficients of the performance function with respect to the original stochastic basic variables X.

After the design point is found, one also is interested in the sensitivity of the reliability index and failure probability with respect to changes in the involved stochastic basic variables. In the uncorrelated standardized normal Z’-space, the sensitivity of в and ps with respect to Z’ can be computed by Eqs. (4.49) and (4.50) with X’ replaced by Z’. The sensitivity of в with respect to X in the original parameter space then can be obtained as

from which the sensitivity for ps can be computed by Eq. (4.50b). A flowchart using the Ang-Tang algorithm for problems involving correlated stochastic basic variables is shown in Fig. 4.12. Step-by-step procedures for the corre­lated normal case by the Hasofer-Lind and Ang-Tang algorithms are given as follows.

The Hasofer-Lind AFOSM algorithm for problems having correlated normal stochastic variables involves the following steps:

Step 1: Select an initial trial solution x(r).

Step 2: Compute W(x(r>) and the corresponding sensitivity coefficient vector

Sx,(r ) *

Step 3: Revise solution point xо+i> according to

Step 4: Check if x(r) and x(r+1) are sufficiently close. If yes, compute the reliability index в(г) according to

в AFOSM — [(x* — fix ) Cx1(xif — fix )]1/2 (4.71)

and the corresponding reliability ps — then, go to step 5. Other­

wise, update the solution point by letting x(r) — x(r+1) and return to step 2.

Step 5: Compute the sensitivity of the reliability index and reliability with respect to changes in stochastic basic variables at the design point x* by Eqs. (4.49), (4.50), (4.69), and (4.58).

On the other hand, the Ang-Tang AFOSM algorithm for problems involving correlated, normal stochastic basic variables consists of following steps:

Step 1: Decompose the correlation matrix Rx to find its eigenvector matrix Vx and eigenvalues Vs, using appropriate techniques.

Step 2: Select an initial point x(r) in the original parameter space.

Step 3: At the selected point x(r) compute the mean and variance of the performance function W(X) according to Eqs. (4.56) and (4.43), respectively.

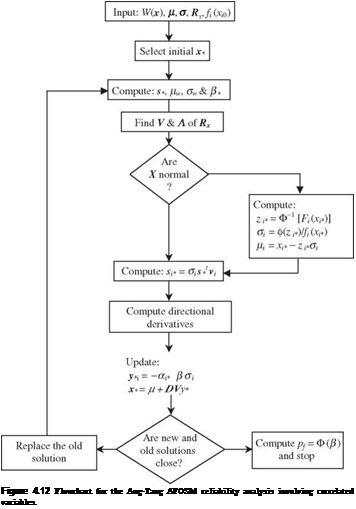
Step 4: Compute the corresponding reliability index ) according to Eq. (4.34).

Step 5: Compute sensitivity coefficients sz> in the uncorrelated standard nor­mal space according to Eq. (4.68) and the vector of directional derivatives a’Xr) according to Eq. (4.67).

Step 6: Using в(г) and ) obtained from steps 4 and 5, compute the location

of expansion point z r +1> in the uncorrelated standard normal space as

Step 7: Convert the obtained expansion point zT +p back to the original pa­rameter space according to Eq. (4.66b).

Step 8: Check if the revised expansion point x(r+p differs significantly from the previous trial expansion point x (r). If yes, use the revised expansion point as the trial point by letting x(r) = x(r+p, and go to step 3 for another iteration. Otherwise, the iteration procedure is considered complete, and the latest reliability index в(г) is used to compute the reliability ps = Ф(во)).

Step 9: Compute the sensitivity of the reliability index and reliability with respect to changes in stochastic basic variables at the design point x+ by Eqs. (4.49), (4.50), (4.69), and (4.68).

Example 4.11 (Correlated, normal) Refer to the data in Example 4.9 for the storm sewer reliability analysis problem. Assume that Manning’s roughness coefficient n and pipe diameter D are dependent normal random variables having a correlation coefficient of -0.75. Furthermore, the pipe slope S also is a normal random variable but is independent of Manning’s roughness coefficient and pipe size. Compute the re­liability that the sewer can convey an inflow discharge of 35 ft3/s by the Hasofer-Lind algorithm.

Solution The initial solution is taken to be the means of the three stochastic basic vari­ables, namely, xq) = p, x = (ц, п, xd, xs/ = (0.015,3.0,0.005/. Since the stochastic basic variables are correlated normal random variables with a correlation matrix as follows:

	1.0	Pn, D	Pn, S		1.00	-0.75	0.00
Rx =	pn, D	1.0	PD, S	=	-0.75	1.00	0.00
	.Pn, S	PD, S	1.0		0.00	0.00	1.00

by the spectral decomposition, the eigenvalues matrix associated with the correlation matrix Rx is Лх = diag(1.75, 0.25, 1.00), and the corresponding eigenvector matrix Vx is

0.7071 0.7071 0.0000 -0.7071 0.7071 0.0000 0.0000 0.0000 1.0000

At x(i) = (0.015, 3.0, 0.005/, the sensitivity vector for the performance function

W(n, D, S) = (QC — Ql) = 0.463П1 D8/3S1/2 — 35

is sx (1) = (9W/дn, dW/дD, dW/дS) = (-2734, 36.50, 4101/

and the value of the performance function W(x(1)) = 6.010, is not equal to zero. This indicates that the solution point x(1) does not lie on the limit-state surface. Applying Eq. (4.70), the new solution x(2) can be obtained as x(2) = (0.01569, 2.900, 0.004885). The difference between the two consecutive solutions is computed as

9 = |x(1) — x(2)| = [(0.01569 — 0.015)2 + (2.9 — 3.0)2 + (0.004885 — 0.005)2]0 5

= 0.1002

which is considered large, and therefore, the iteration continues. The following table lists the solution point x(r), its corresponding sensitivity vector sx,(r), and the vector of directional derivatives azi,(r), in each iteration. The iteration stops when the Eu­clidean distance between the two consecutive solution points is less than 0.001 and the value of the performance function is less than 0.001.

Iteation	Var.	x (r )	s (r )	a(r)	x(r+1)
r = 1	n	0.1500 x 10—01	—0.2734 x 10+04	—0.9681 x 10+00	0.1599 x 10—01
	D	0.3000 x 10+01	0.3650 x 10+02	0.2502 x 10+00	0.2920 x 10+01
	S	0.5000 x 10—02	0.4101 x 10+04	0.1203 x 10—01	0.4908 x 10—02
	s	= 0.8008 x 10—01	W = 0.6010 x 10+01	в = 0.000 x 10+00
r = 2	n	0.1599 x 10—01	—0.2217 x 10+04	—0.9656 x 10+00	0.1607 x 10—01
	D	0.2920 x 10+01	0.3242 x 10+02	0.2583 x 10+00	0.2912 x 10+01
	S	0.4908 x 10—02	0.3612 x 10+04	0.2857 x 10—01	0.4897 x 10—02
	s =	0.7453 x 10 — 02	W = 0.4565 x 10+00	в = 0.1597 x 10+01
r = 3	n	0.1607 x 10—01	—0.2178 x 10+04	—0.9654 x 10+00	0.1607 x 10—01
	D	0.2912 x 10+01	0.3209 x 10+02	0.2591 x 10+00	0.2912 x 10+01
	S	0.4897 x 10—02	0.3574 x 10+04	0.2991 x 10—01	0.4896 x 10—02
	s	= 0.7101 x 10—04	W = 0.2992 x 10—02	в = 0.1598 x 10+01

After four iterations, the solution converges to the design point x* = (n*, D*, S*)f = (0.01607, 2.912, 0.004896)г. At the design point x*, W = 0.5 7 5 8 x 10—07, and the mean and standard deviation of the performance function W can be estimated, by Eqs. (4.42) and (4.43), respectively, as

jlw* — 5.510 and &w* — 3.448

The reliability index then can be computed as в* = pw* /aw* = 1.598, and the corre­sponding reliability and failure probability can be computed, respectively, as

ps = Ф(в*) = 0.9450 pf = 1 — ps = 0.055

Finally, at the design point x*, the sensitivity of the reliability index and reliabil­ity with respect to each of the three stochastic basic variables can be computed by Eqs. (4.49), (4.50), (4.56), and (4.57). The results are shown in the following table:

Variable (1)	x (2)	a* (3)	дв/д z (4)	д Ps/д z (5)	дв/д x (6)	д ps/д x (7)	хдв/вдx (8)	xд ps / Psд x (9)
n	0.01607	—0.9654	0.9654	0.1074	690.3	76.81	11.09	1.234
D	2.912	0.2591	—0.2591	—0.02883	—119.6	—13.31	—348.28	—38.76
S	0.004896	0.02991	—0.02991	—0.003328	—1814.	—201.9	—8.881	—0.9885