Total probability theorem and Bayes’ theorem

The probability of the occurrence of an event E, in general, cannot be deter­mined directly or easily. However, the event E may occur along with other attribute events Ak. Referring to Fig. 2.2, event E could occur jointly with K mutually exclusive (Aj П Ak — 0 for j — k) and collectively exhaustive (A1 U A2 U—U AK) — S attributes Ak, k — 1,2,…, K. Then the probability of the occur­rence of an event E, regardless of the attributes, can be computed as

KK

P(E) — P(E, Ak) — P (E | Ak)P(Ak) (2.8)

k—1 k—1

Equation (2.8) is called the total probability theorem.

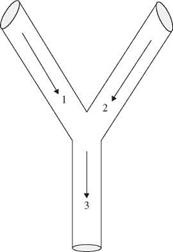
Example 2.4 Referring to Fig. 2.3, two upstream storm sewer branches (I1 and I2) merge to a sewer main (I3). Assume that the flow-carrying capacities of the two up­stream sewer branches I1 and I2 are equal. However, hydrologic characteristics of the contributing drainage basins corresponding to I1 and I2 are somewhat differ­ent. Therefore, during a major storm event, the probabilities that sewers I1 and I2 will exceed their capacities (surcharge) are 0.5 and 0.4, respectively. For simplicity, assume that the occurrences of surcharge events in the two upstream sewer branches are independent of each other. If the flow capacity of the downstream sewer main I3 is

S

Figure 2.2 Schematic diagram of total probability theorem.

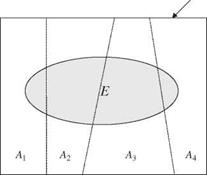
Figure 2.3 A system with three sewer sections.

the same as its two upstream branches, what is the probability that the flow capacity of the sewer main I3 will be exceeded? Assume that when both upstream sewers are carrying less than their full capacities, the probability of downstream sewer main I3 exceeding its capacity is 0.2.

Solution Let E1, E2, and E3, respectively, be events that sewer I1, I2, and I3 exceed their respective flow capacity. From the problem statements, the following probabili­ties can be identified: P(E1) = 0.50, P(E2) = 0.40, and P(E3 | E1, E’2) = 0.2.

To determine P(E3), one first considers the basic events occurring in the two up­stream sewer branches that would result in surcharge in the downstream sewer main E3. There are four possible attribute events that can be defined from the flow con­ditions of the two upstream sewers leading to surcharge in the downstream sewer main. They are A1 = (E1, E2), A2 = (E1, E2), A3 = (E1, E2), and A4 = (E1, E2). Fur­thermore, the four events A1, A2, A3, and A4 are mutually exclusive.

Since the four attribute events A1, A2, A3, and A4 contribute to the occurrence of event E3, the probability of the occurrence of E3 can be calculated, according to Eq. (2.8), as

P(E3) = P(E3, A1) + P(E3, A2) + P(E3, A3) + P(E3, A4)

= P(E3 | A1)P(A1) + P(E3 | A2)P(A2) + P(E3 | A3)P(A3) + P(E3 | A4)P(A4)

To solve this equation, each of the probability terms on the right-hand side must be identified. First, the probability of the occurrence of A1, A2, A3, and A4 can be determined as the following:

P(A1) = P(E1, E2) = P(E1) x P(E2) = (0.5)(0.4) = 0.2

The reason that P (E1, E2) = P (E1) x P (E2) is due to the independence of events E1 and E2. Since E1 and E2 are independent events, then E1, E1, E2, and E2 are also

independent events. Therefore,

P(A2) = P(E, E2) = P() x P(E2) = (1 — 0.5)(0.4) = 0.2

P(A3) = P(E1, E2) = P(E1) x P(E2) = (0.5)(1 — 0.4) = 0.3

P(A4) = P(E1, E2) = P(E1) x P(E2) = (1 — 0.5)(1 — 0.4) = 0.3

The next step is to determine the values of the conditional probabilities, that is, P(E3 | A1), P(E3 | A2), P(E3 | A3), and P(E3 | A4). The value of P(E3 | A4) = P(E3 | E’, E2) = 0.2 is given by the problem statement. On the other hand, the values of the remaining three conditional probabilities can be determined from an understanding of the physical process. Note that from the problem statement the downstream sewer main has the same conveyance capacity as the two upstream sewers. Hence any up­stream sewer exceeding its flow-carrying capacity would result in surcharge in the downstream sewer main. Thus the remaining three conditional probabilities can be easily determined as

P(E3 | A1) = P(E3 | E1, E2) = 1.0 P(E3 | A2) = P(E3 | E1, E2) = 1.0 P(E3 | A3) = P(E3 | E1, E2) = 1.0

Putting all relevant information into the total probability formula given earlier, the probability that the downstream sewer main I3 would be surcharged in a major storm is

P(E3) = P(E3 | A1)P(A1) + P(E3 | A2)P(A2) + P(E3 | A3)P(A3) + P(E3 | A4)P(A4)

= (1.0)(0.2) + (1.0)(0.2) + (1.0)(0.3) + (0.2)(0.3)

= 0.76

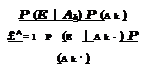The total probability theorem describes the occurrence of an event E that may be affected by a number of attribute events Ak, k = 1, 2,…, K. In some situations, one knows P (E | Ak) and would like to determine the probability that a particular event Ak contributes to the occurrence of event E. In other words, one likes to find P(Ak | E). Based on the definition of the conditional probability (Eq. 2.6) and the total probability theorem (Eq. 2.8), P (Ak | E) can be computed as

Equation (2.9) is called Bayes’ theorem, and P (Ak) is the prior probability, rep­resenting the initial belief of the likelihood of occurrence of attribute event Ak. P (E | Ak) is the likelihood function, and P (Ak | E) is the posterior probability, representing the new evaluation of Ak being responsible in the light of the oc­currence of event E. Hence Bayes’ theorem can be used to update and revise the calculated probability as more information becomes available.

Example 2.5 Referring to Example 2.4, if surcharge is observed in the downstream storm sewer main I3, what is the probability that the incident is caused by simulta­neous surcharge of both upstream sewer branches?

Solution From Example 2.4, A1 represents the event that both upstream storm sewer branches exceed their flow-carrying capacities. The problem is to find the conditional probability of A1, given that event E3 has occurred, that is, P(A1 | E3). This condi­tional probability can be expressed as

From Example 2.4, the numerator and denominator of the preceding conditional prob­ability can be computed as

The original assessment of the probability is 20 percent that both upstream sewer branches would exceed their flow-carrying capacities. After an observation of down­stream surcharge from a new storm event, the probability of surcharge occurring in both upstream sewers is revised to 26.3 percent.