Time-Dependent Reliability Models
The development of hydrosystems engineering projects often includes the design of various types of hydraulic structures, such as pipe networks for water supply, storm sewer systems for runoff collection, levee and dike systems for flood control and protection, and others. Generally, the system, once designed and constructed, is expected to serve its intended objectives over a period of several years, during which the system behavior and environmental factors could change with respect to time. In such circumstances, engineers often are interested in evaluating the reliability of the hydraulic structure with respect to a specified time framework. For example, one might be interested in the risk of overflow of an urban storm water detention basin in the summer when convective thunderstorms prevail. Loads to most hydrosystems are caused by the occurrence of hydrologic events such as floods, storms, or droughts that are random by nature. Time-dependent reliability analysis considers repeated applications of loads and also can consider the change of the distribution of resistance with time.
In preceding sections, emphasis was placed on static reliability analysis, which does not consider the time dependency of the load and resistance. This section considers the time-dependent random variables in reliability analysis. As a result, the reliability is a function of time, i. e., time dependent or time variant. The difference between the time-to-failure analysis described in Chap. 6 and the time-dependent reliability analysis should be pointed out. The commonality between the two reliability analyses is that both attempt to assess the variation of reliability with respect to time. The difference lies in the manner in which the reliability is computed. Time-to-failure analysis is concerned
only with the time history of the performance of the system as a whole without giving explicit consideration to the load-resistance interference as done by time – dependent reliability analysis. The objective of time-dependent reliability models is to determine the system reliability over a specified time interval in which the number of occurrences of loads is a random variable.
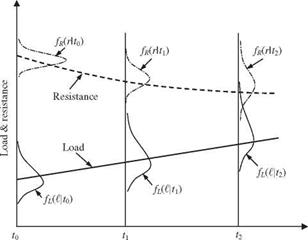
When both loading and resistance are functions of time, the performance function W(t) = R(t) – L(t) is time-dependent. Consequently, the reliability Ps(t) = P [W(t) > 0] would vary with respect to time. Figure 4.19 shows schematically the key feature of the time-dependent reliability problem in which the PDFs of load and resistance change with time. In Fig. 4.19, the mean of resistance has a downward trend with time, whereas that of the load increases with time. As the standard deviations of both resistance and load increase with time, the area of interference increases, and this results in an increase in the failure probability with time. The static reliability analysis described in preceding sections considers neither load nor resistance being functions of time.
If the load is to be applied many times, it is often the largest load that is considered in reliability analysis. Then this maximum load can be described by an extreme-value distribution such as the Gumbel distribution described in Sec. 2.6.4. In doing so, the effect of time is ignored in reliability analysis, which may not be appropriate, especially when more than one load is involved or the resistance changes with time. A comprehensive treatment of time-dependent reliability issues can be found in Melchers (1999).
|
Time t Figure 4.19 Time-dependence of load and resistance probability distribution functions. |






Leave a reply