Reliability computations for time-dependent models can be made for deterministic and random cycle times. The development of a model for deterministic cycles is given first, which naturally leads to the model for random cycle times.
Number of occurrences is deterministic. Consider a hydrosystem with a fixed resistance (or capacity) R = r subject to n repeated loads L1, L2,…, Ln. When the number of loads n and system capacity r are fixed, the reliability of the system after n loadings ps(n, r) can be expressed as
Ps(n, r ) = P [(L1 < r ) n (L2 < r ) П—П (Ln < r )] = P (Lmax < Г ) (4.100)
where Lmax = max{L1, L2,…, Ln}, which also is a random variable. If all random loadings L are independent with their own distributions, Eq. (4.100) can be written as
Ps(n, r) = [FLi(r)] (4.101)
i=1
where FLi (r) is the CDF of the ith load. In the case that all loadings are generated by the same statistical process, that is, all Ls are identically distributed with FLi(r) = FL(r), for i = 1, 2,…, n, Eq. (4.101) can further be reduced to
Ps(n, r) = [FL(r )]
 |
 |
 |
If the resistance of the system also is a random variable, the system reliability under the fixed number of loads n can be expressed as
Number of occurrences is random. Since the loadings to hydrosystems are related to hydrologic events, the occurrence of the number of loads, in general, is uncertain. The reliability of the system under random loading in the specified time interval [0, t] can be expressed as
TO
Ps(t) = n (t |n) Ps(n)
n=0
in which n(t |n) is the probability of n loadings occurring in the time interval [0, t]. A Poisson distribution can be used to describe the probability of the number of events occurring in a given time interval. In fact, the Poisson distribution has been found to be an appropriate model for the number of occurrences of hydrologic events (Clark, 1998; Todorovic and Yevjevich, 1969; Zelenhasic, 1970). Referring to Eq. (2.55), n(t |n) can be expressed as
e Xt ( X t )n
n (t |n) =————- (— (4.105)
n!
where X is the mean rate of occurrence of the loading in [0, t], which can be estimated from historical data.
Substituting Eq. (4.105) in Eq. (4.104), the time-dependent reliability for the random independent load and random-fixed resistance can be expressed as
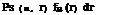
(4.106)
Under the condition that random loads are independently and identically distributed, Eq. (4.106) can be simplified as
n TO
Ps (t) = e- t [1-FL(r)] fR (r) dr (4.107)
0
