Statistical Properties of Random Variables

In statistics, the term population is synonymous with the sample space, which describes the complete assemblage of all the values representative of a partic­ular random process. A sample is any subset of the population. Furthermore, parameters in a statistical model are quantities that are descriptive of the pop­ulation. In this book, Greek letters are used to denote statistical parameters. Sample statistics, or simply statistics, are quantities calculated on the basis of sample observations.

2.1.3 Statistical moments of random variables

In practical statistical applications, descriptors commonly used to show the sta­tistical properties of a random variable are those indicative of (1) the central tendency, (2) the dispersion, and (3) the asymmetry of a distribution. The fre­quently used descriptors in these three categories are related to the statistical moments of a random variable. Currently, two types of statistical moments are used in hydrosystems engineering applications: product-moments and L-moments. The former is a conventional one with a long history of practice, whereas the latter has been receiving great attention recently from water re­sources engineers in analyzing hydrologic data (Stedinger et al., 1993; Rao and Hamed 2000). To be consistent with the current general practice and usage, the terms moments and statistical moments in this book refer to the conventional product-moments unless otherwise specified.

Product-moments. The r th-order product-moment of a random variable X about any reference point X = xo is defined, for the continuous case, as

/

СО /* CO

(x — xo)r fx(x) dx = / (x — xo)r dFx(x) (2.20a)

-O J — O

whereas for the discrete case,

K

E [(X — xo)r ] = ]T (xk — xo )rpx (xk) (2.20b)

k = і

where E [■] is a statistical expectation operator. In practice, the first three mo­ments (r = 1,2, 3) are used to describe the central tendency, variability, and asymmetry of the distribution of a random variable. Without losing generality, the following discussions consider continuous random variables. For discrete random variables, the integral sign is replaced by the summation sign. Here it is convenient to point out that when the PDF in Eq. (2.20a) is replaced by a conditional PDF, as described in Sec. 2.3, the moments obtained are called the conditional moments.

Since the expectation operator E [ ] is for determining the average value of the random terms in the brackets, the sample estimator for the product-moments for p’r = E(Xr), based on n available data (x1, x2,…, xn), can be written as

n

p’r = ^2 wi (n) xr (2.21)

i = 1

where wi(n) is a weighting factor for sample observation xi, which depends on sample size n. Most commonly, wi(n) = 1/n, for all i = 1, 2,…, n. The last column of Table 2.1 lists the formulas applied in practice for computing some commonly used statistical moments.

Two types of product-moments are used commonly: moments about the ori­gin, where xo = 0, and central moments, where xo = px, with px = E[X]. The r th-order central moment is denoted as pr = E [(X — px )r ], whereas the r th — order moment about the origin is denoted as p’r = E(Xr). It can be shown easily, through the binomial expansion, that the central moments pr = E [(X — px)r ] can be obtained from the moments about the origin as

r

pr = ]T( —1)fCr, i p’x ri—i (2.22)

i = 0

where Cr, i = (r) = i!(/^is a binomial coefficient, with! representing factorial, that is, r! = r x (r — 1) x (r — 2) x-x 2 x 1. Conversely, the moments about the origin can be obtained from the central moments in a similar fashion as

r

jXr = ‘У ^ Cr, i №x №r —i (2.23)

i = 0

Moment Measure of Definition Continuous variable Discrete variable Sample estimator First Central Mean, expected value Vx = f ° xfx(x) dx Vx = Eallx’s xkP(xk ) x = E xi/n location E( X) = Vx Second Dispersion Variance, Var(X) = V2 = °X ax = /Too (x — Vx)2 f x(x) dx °x = Eallx’s(xk — Vx)2 Px(xk ) s2 = n-1 E(xi — x)2 Standard deviation, ax ax = у/Var( X) ax = у/Var( X) s=J n-л E( xi — x)2 Coefficient of variation, &x £2x = ax/vx £2x = ax/Vx Cv = s/x Third Asymmetry Skewness V3 = f-T (x — Vx )3 fx(x) dx V3 = ^ ^all x’s (xk — Vx ) px(xk ) m3 = (n-1)(n-2) E (x x) Skewness coefficient, yx Yx = V3/a£ Yx = V3 /a£ g = m3/s’3 Fourth Peakedness Kurtosis, кх V4 = 1° (x — Vx )4 fx(x) dx V4 = allx’s (xk — V%)4px(xk ) m4 = (n-l)(n-2)(n-3) E(x x) Excess coefficient, Ex Kx = V4/a£ Kx = V4/a£ k = m4/s4 єx — Kx 3 Єx — Kx 3

Equation (2.22) enables one to compute central moments from moments about the origin, whereas Eq. (2.23) does the opposite. Derivations for the expressions of the first four central moments and the moments about the origin are left as exercises (Problems 2.10 and 2.11).

The main disadvantages of the product-moments are (1) that estimation from sample observations is sensitive to the presence of extraordinary values (called outliers) and (2) that the accuracy of sample product-moments deteriorates rapidly with an increase in the order of the moments. An alternative type of moments, called L-moments, can be used to circumvent these disadvantages.

Example 2.8 (after Tung and Yen, 2005) Referring to Example 2.6, determine the first two moments about the origin for the time to failure of the pump. Then calculate the first two central moments.

Solution From Example 2.6, the random variable T is the time to failure having an exponential PDF as

ft(t) = ^ exp(-1/1250) for t > 0, в> 0

in which t is the elapsed time (in hours) before the pump fails, and в = 1250 h/failure.

The moments about the origin, according to Eq. (2.20a), are

r / e-t/e

E (Tr) = t4 = J t4—J dt

Using integration by parts, the results of this integration are for r = 1, p^ = E(T ) = pt = в = 1250 h

for r = 2, p’2 = E(T 2) = 2в2 = 3,125,000 h2

Based on the moments about the origin, the central moments can be determined, according to Eq. (2.22) or Problem (2.10), as

for r = 1, P1 = E (T — pt) = 0

for r = 2, p2 = E [(T — pt )2] = p’2 — P2 = 2в2 — в2 = в2 = 1, 562, 500 h2

L-moments. The r th-order L-moments are defined as (Hosking, 1986, 1990)

Xr = 1 ^ (—1)j— ^ E (— j r) r = 1,2,… (2.24)

in which Xj :n is the j th-order statistic of a random sample of size n from the

distribution Fx(x), namely, X(1) < X(2) < ■ ■ ■ < X(j) < — < X(n). The “L” in L-moments emphasizes that Xr is a linear function of the expected order statis­tics. Therefore, sample L-moments can be made a linear combination of the ordered data values. The definition of the L-moments given in Eq. (2.24) may appear to be mathematically perplexing; the computations, however, can be sim­plified greatly through their relations with the probability-weighted moments,
which are defined as (Greenwood et al., 1979)

xr [Fx(x)]p [1 — Fx(x)]q dFx(x)

(2.25)

Compared with Eq. (2.20a), one observes that the conventional product — moments are a special case of the probability-weighted moments with p = q = 0, that is, Mr,0,0 = g’r. The probability-weighted moments are particularly attractive when the closed-form expression for the CDF of the random variable is available.

To work with the random variable linearly, M1,p, q can be used. In particu­lar, two types of probability-weighted moments are used commonly in practice, that is,

ar = M1,0,r = E{X[1 — Fx(X)]r} r = 0,1,2,… (2.26a)

вг = M1,r,0 = E{X[Fx(X)]r} r = 0,1,2,… (2.26b)

In terms of ar or er, the r th-order L-moment Xr can be obtained as (Hosking,

1986)

Xr + 1 = ( -1)rJ2 Pr, j a j =Yj Pr, j ej r = 0,1 …

j = 0 j = 0

in which

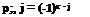rfr + i (-1)r j (r + j )!

JA j J (j!)2(r — j)!

For example, the first four L-moments of random variable X are

X1 — e0 — g-1 — gx	(2.28a)
X2 = 2в1 — в0	(2.28b)
X3 = 6в2 — 6в1 + в0	(2.28c)
X4 = 20вэ — 30в2 + 12в1 — в0	(2.28d)

To estimate sample a — and в-moments, random samples are arranged in as­cending or descending order. For example, arranging n random observations in ascending order, that is, X(1) < X(2) < ■ ■ ■ < X(j) < ■ ■ ■ < X(n), the rth-order в-moment er can be estimated as

1n

er = -]T X(i) F (X(i))r (2.29)

n

i = 1

where F(X(i)) is an estimator for F(X(i>) = P(X < X(i>), for which many plotting-position formulas have been used in practice (Stedinger et al., 1993).

The one that is used often is the Weibull plotting-position formula, that is,

F (X (i)) = i / (n + 1).

L-moments possess several advantages over conventional product-moments. Estimators of L-moments are more robust against outliers and are less biased. They approximate asymptotic normal distributions more rapidly and closely. Although they have not been used widely in reliability applications as com­pared with the conventional product-moments, L-moments could have a great potential to improve reliability estimation. However, before more evidence be­comes available, this book will limit its discussions to the uses of conventional product-moments.

Example 2.9 (after Tung and Yen, 2005) Referring to Example 2.8, determine the first two L-moments, that is, Л1 and Л2, of random time to failure T.

Solution To determine Л1 and Л2, one first calculates 0o and 01, according to Eq. (2.26b), as

0 = E{T [Ft(T)]0} = E(T) = nt = в

01 =

00 From Eq. (2.28), the first two L-moments can be computed as

60 0

Л2 = 201 — 00 = —— 0 = —