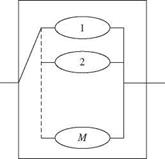 |
 |
A standby redundant system is a parallel system in which only one component or subsystem is in operation (Fig. 7.7). It is a special case of K-out-of-M system with K = 1. If the operating component fails, then another component is operated. This type of system is different than the parallel system described in Sec. 7.3.2, where all components are concurrently operating because standby
 |
 |
units do not operate. The system reliability for a system with M components out of which M — 1 units are on standby is the probability that at most M — 1 components fail. This probability can be expressed by
 |
 |
 |
|
 |
 |
Note that this equation is valid under the following assumptions: The switching arrangement is perfect, the units are identical, the component failure rates are constant, the standby units are as good as new, and the unit failures are statistically independent. The mean time to failure of the system can be obtained, according to Eq. (5.18), as
Equation (7.62) is intuitively obvious in that the system’s operation is the result of a relay of a series of components. As one component fails, the second one comes to operation until failure occurs. Therefore, the system MTTF is the sum of the MTTFs of individual components.
Example 7.11 As an example of a standby redundant system, assume an exponential failure distribution for two identical pumps, one operating and the second on standby, with identical failure rates of X = 0.0005 failures/h. The standby unit is as good as new at time t = 0. The system reliability for t = 1000 h is
ps, sys(t = 1000) = [1 + (0.0005)(1000)]e—(00005)(1000) = 0.9098
