Some One-Dimensional Numerical Integration Formulas

This appendix summarizes some commonly used numerical formulas for eval­uating the following integral:

Detailed descriptions of these and other numerical integration procedures can be found in any numerical analysis textbook.

4A.1 Trapezoidal rule

For a closed integral, Eq. (4A.1) can be approximated as

1 = hif 1 + 2 Щ fi + (4A.2a)

where h is a constant space increment for discretization, n is the number of discretization points over the interval (a, b), including the two end points, and fi is the function values at discretized point, xi.

For open and semiopen integrals, Eq. (4A.1) can be computed numerically as

1 = h (эf2 + 2£ fi + 3fn-1^ (4A.2b)

4A.2 Simpson’s rule

For closed integrals, one has

h

1 = 3 [ f 1 + 4( f 2 + f 4 + f 6 + ■ ■ •) + 2( f 3 + f 5 + f 7 + •• •) + fn] (4A.3a)

For open and semiopen integrals, one has

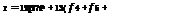•) + 16( f 5 + f 7 + ■ ■ •) + 27f n-1] (4A.3b)

4A.3 Gaussian quadratures

Equation (4A.1) can be expressed as

n

1 = wif (Xi) (4A.4)

i=1

where wi is the weight associated with the ith abscissa xi in the discretiza­tion. The weight wi is related to orthogonal polynomials. Table 4A.1 lists some commonly used orthogonal polynomials and their applied integral range, ab­scissas, and weights. Definitions of those polynomials and tables of abscissas and weights for different Gaussian quadratures are given by Abramowitz and Stegun (1972).

TABLE 4A.1 Some Commonly Used Gaussian Quadratures

Gauss Range (a, b) Abscissas Xf Weight wi

in which lkj and akj are elements in matrices L and A, respectively, and K is the size of the matrices. In terms of akj’s, lkj’s can be expressed as

k-1

lkk — I akk ^ ^ lkj

j—1

Computationally, the values of lkj’s can be obtained by solving Eqs. (4B.4) and (4B.5) sequentially following the order k — 1,2,…, K. Numerical examples can be found in Wilkinson (1965, p. 71). A simple computer program for the Cholesky decomposition is available from Press et al. (1992, p. 90). Note that the requirement of positive definite for matrix A is to ensure that the quantity in the square root of Eq. (4B.4) always will be positive throughout the computation. If A is not a positive-definite matrix, the algorithm will fail.

For a real, symmetric, positive-definite matrix A, the Cholesky decomposition is sometimes expressed as

A — L Л Lt (4B.6)

in which L is a unit lower triangular matrix with all its diagonal elements having values of ones, and Л is a diagonal eigenvalue matrix. Therefore, the eigenvalues associated with matrix A are the square roots of the diagonal el­ements in matrix L. If a matrix is positive-definite, all its eigenvalues will be positive, and vice versa.

In theory, the covariance and correlation matrices in any multivariate prob­lems should be positive-definite. In practice, sample correlation and sample covariance often are used in the analysis. Owing to the sampling errors, the resulting sample correlation matrix may not be positive-definite, and in such cases, the Cholesky decomposition may fail, whereas the spectral decomposition described in Appendix 4C can be applicable.