Repair rate and its relationship with repair density and repair probability

The repair rate r (t), similar to the failure rate, is the conditional probability that the system is repaired per unit time given that the system failed at time zero and is still not repaired at time t. The quantity r (t) dt is the probability that the system is repaired during the time interval (t, t + dt] given that the system fails at time t. Similar to Eq. (5.3), the relationship among repair density function, repair rate, and repair probability is

r (t 1=t—GW,5-22’

Given a repair rate r (t), the repair density function and the maintainability can be determined, respectively, as

г c t -|

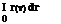
gt(t) = r (t) X exp

5.1.2 Mean time to repair, mean time between failures, and mean time between repairs

The mean time to repair (MTTR) is the expected value of time to repair of a failed system, which can be calculated by

n TO n TO

MTTR = rgt (r) dr = [1 — Gt (r)] d r (5.25)

00

The MTTR measures the elapsed time required to perform the maintenance op­eration and is used to estimate the downtime of a system. The MTTR values for some components in a water distribution system are listed in the last columns of Tables 5.2 and 5.3. It is also a commonly used measure for the maintainability of a system.

The MTTF is a proper measure of the mean life span of a nonrepairable system. However, for a repairable system, the MTTF is no longer appropriate for representing the mean life span of the system. A more representative indicator for the fail-repair cycle is the mean time between failures (MTBF), which is the sum of MTTF and MTTR, that is,

MTBF = MTTF + MTTR (5.26)

The mean time between repairs (MTBR) is the expected value of the time be­tween two consecutive repairs, and it is equal to MTBF. The MTBF for some typ­ical components in a water distribution system are listed in Tables 5.2 and 5.3.

Example 5.6 Consider a pump having a failure density function of ft(t) = 0.0008exp(-0.0008t) fort > 0

and a repair density function of

gt(t) = 0.02 exp(-0.02t) for t > 0

in which t is in hours. Determine the MTBF for the pump.

Solution To compute the MTBF, the MTTF and MTTR of the pump should be calcu­lated separately. Since the time to failure and time to repair are exponential random variables, the MTTF and MTTR, respectively, are

MTTF = 1/0.0008 = 1250 hours

MTTR = 1/0.02 = 50 hours

Therefore, MTBF = MTTF + MTTR = 1250 + 50 = 1300 hours.