Relationships among failure density function, failure rate, and reliability

According to Eq. (5.3), given the failure density function ft(t) it is a straight­forward task to derive the failure rate h(t). Furthermore, based on Eq. (5.3), the reliability can be computed directly from the failure rate as

Substituting Eq. (5.10) into Eq. (5.3), the failure density function ft(t) can be expressed in terms of the failure rate as

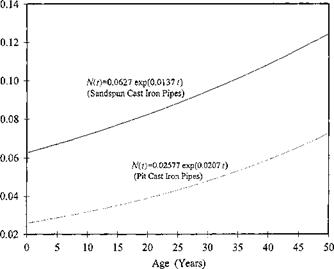
Example 5.3 (after Mays and Tung, 1992) Empirical equations have been developed for the break rates of water mains using data from a specific water distribution system. As an example, Walski and Pelliccia (1982) developed break-rate equations for the water distribution system in Binghamton, New York. These equations are

Pit cast iron: N(t) = 0.02577e00207t

Sandspun cast iron: N(t) = 0.0627e00137t

where N (t) is the break rate (in number of breaks per mile per year), and t is the age of the pipe (in years). The break rates versus the ages of pipes for the preceding two types of cast iron pipes are shown in Fig. 5.9. Derive the expressions for the failure rate, reliability, and failure density function for a 5-mile water main of sandspun cast iron pipe.

Solution The break rate per year (i. e., failure rate or hazard function for the 5-mile water main) for sandspun cast iron pipe can be calculated as

h(t) = 5 miles x N(t) = 0.3185e00137t

The reliability of this 5-mile water main then can be computed using Eq. (5.10) as ps(t) = exp^- J 0.3185e0 0137T d^j = exp[23.25(1 — e00137t)]

Figure 5.9 Break-rate curves for sandspun cast iron and pit cast iron pipes.

ft(t) = 0.3185e00137t x exp[23.25(1 — e00137t)]

The curves for the failure rate, reliability, and failure density function of the 5-mile sandspun cast iron water main are shown in Fig. 5.10.