Path enumeration method
This is a very powerful method for system reliability evaluation. A path is defined as a set of components or modes of operation that leads to a certain outcome of the system. In system reliability analysis, the system outcomes of interest are those of failed state or operational state. A minimum path is one in which no component is traversed more than once in going along the path. Under this methodologic category, tie-set analysis and cut-set analysis are two well-known techniques.
Cut-set analysis. The cut set is defined as a set of system components or modes of operation that, when failed, cause the failure of the system. Cut-set analysis is powerful for evaluating system reliability for two reasons: (1) It can be programmed easily on digital computers for fast and efficient solutions of any general system configuration, especially in the form of a network, and (2) the cut sets are directly related to the modes of system failure and therefore identify the distinct and discrete ways in which a system may fail. For example, in a water distribution system, a cut set will be the set of system components including pipe sections, pumps, storage facilities, etc. that, when failed jointly, would disrupt the service to certain users.
The cut-set method uses the minimum cut sets for calculating the system failure probability. The minimum cut set is a set of system components that, when all failed, causes failure of the system but when any one component of the set does not fail does not cause system failure. A minimum cut set implies that all components of the cut set must be in the failure state to cause system failure. Therefore, the components or modes of operation involved in the minimum cut set are effectively connected in parallel, and each minimum cut set is connected in series. Consequently, the failure probability of a system can be expressed as
in which Cm is the mth of the total I minimum cut sets, Jm is the total number of components or modes of operation in the mth minimum cut set, and Fmj represents the failure event associated with the j th components or mode of operation in the mth minimum cut set. In the case that the number of minimum
cut sets I is large, computing the bounds for probability of a union described in Sec. 7.2.3 can be applied. The bounds on the failure probability of the system should be examined for their closeness to ensure that adequate accuracy is obtained.
Example 7.13 Refer to the simple water distribution network shown in Fig. 7.9 in Example 7.12. Evaluate the system reliability using the minimum cut-set method.
Solution Based on the system reliability as defined, the minimum cut sets for the example pipe network are
C1 : F1 C2 : F2 П F3 C3 : F2 П F4 C4 : F3 П F5
C5 : F4 П F5 C6 : F2 П F5 C7 : F3 П F4
where Cm is the mth cut set, and Fk is the failure state of pipe link k. The seven cut sets for the example network listed above are shown in Fig. 7.11. The system unreliability pf, sys is the probability of occurrence of the union of the cut set, that is,
Pf, sys = P U Cm
m=1
The system reliability can be obtained by subtracting pf, sys from 1. However, the computation, in general, will be very cumbersome for finding the probability of the
|
|
|
|
|
![]()
![]()
Cm = The mth cut set
union of large numbers of events, even if they are independent. In this circumstance, it is computationally easier to compute the system reliability as
Ps, sys = 1 — P ( U Cmj = P ( n Cm m=1 J m=1
Since all the cut sets behave independently, all their complements also behave independently. The probability of the intersection of a number of independent events, according to Eq. (2.5), is
![]() ps, sys = p( n C’r^j = ^ P(C’m) m=1 /
ps, sys = p( n C’r^j = ^ P(C’m) m=1 /
![]() P (C1) = 0.95 P (C2) = P (C3) = ••• = P (C’7) = 0.9975
P (C1) = 0.95 P (C2) = P (C3) = ••• = P (C’7) = 0.9975
Hence the system reliability of the example water distribution network is ps, sys = (0.95)(0.9975)6 = 0.9360
Tie-set analysis. As the complement of a cut set, a tie set is a minimal path of the system in which system components or modes of operation are arranged in series. Consequently, a tie set fails if any of its components or modes of operation fail. All tie sets are effectively connected in parallel; that is, the system will be in the operating state if any of its tie sets are functioning. Therefore, the system reliability can be expressed as
in which T m is the mth tie set of all I tie sets, Jm is the total number of components or modes of operation in the mth tie set, and F’mj represents the nonfailure state of the j th component in the mth tie set. Again, when the number of tie sets is large, computation of exact system reliability by Eq. (7.64) could be cumbersome. In such a condition, bounds for system reliability could be computed.
The main disadvantage of the tie-set method is that failure modes are not directly identified. Direct identification of failure modes is sometimes essential if a limited amount of a resource is available to focus on a few dominant failure modes.
Example 7.14 Refer to the simple water distribution network as shown in Fig. 7.9. Use tie-set analysis to evaluate the system reliability.
Solution The minimum tie sets (or path), based on the definition of system reliability given previously, for the example network are
T1 : F1 n F2 n F’4 n F5 T 2 : F1 n F3 n F4 n F5 T 3 : F1 n F2 n F3 n F4 T 4 : F1 n F2 n F3 n F5
where T m is the mth minimum tie set, and F j is the nonfailure of the j th pipe link in the network. The four minimum tie sets are shown in Fig. 7.12. The system reliability, based on Eq. (7.64), is
Ps, sys — P(T 1 U T2 U T3 U T4)
= [P(T1) + P(T2) + P(T3) + P(T4)] – [P(T1, T2) + P(T1, T3)
+ P(T1, T4) + P(T2, T3) + P(T2, T4) + P(T3, T4)]
+ [P(T1, T2, T3) + P(T1, T2, T4) + P(T1, T3, T4) + P(T2, T3, T4)] – P(T1, T2, T3, T4)
Since all pipes in the network behave independently, all minimum tie sets behave independently. In such circumstances, the probability of the joint occurrence of multiple independent events is simply equal to the multiplication of the probability of the individual events. That is,
P (T1) — P (F1) P (F2) P (F4) P (F,5) — (0.95)4 — 0.81451
![]()
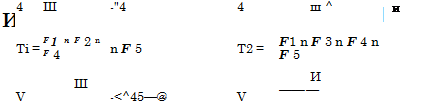 |
|
Ъ————© ъ
T4 = F1 п F 2 n F 3 п F 5
lm = The mth tie set
FJ = Nonfailure state of pipe section j
Similarly,
P (T 2) = P (T 3) = P (T 4) = 0.81451
Note that in this example the unions of more than two minimum tie sets are the intersections of the nonfailure state of all five pipe sections. For example, T1 U T 2 =
(F1 П F2 n F4 П F5) U (F1 n F3 П F4 П F5) = (F1 n F2 n F3 n F4 П F5). The system reliability can be reduced to
Pssys = [P(T1) + P(T2) + P(T3) + P(T4)] – 3P(F1 n F2 n F3 n F4)
= 4(0.81451) – 3(0.95)5 = 0.9367
In summary, the path enumeration method involves the following steps (Henley and Gandhi, 1975):
1. Find all minimum paths. In general, this has to be done with the aid of a computer when the number of components is large and the system configuration is complex.
2. Find all required unions of the paths.
3. Give each path union a reliability expression in terms of module reliability.
4. Compute the system reliability in terms of module reliabilities.






Leave a reply