Parallel systems
For a parallel system, the entire system would perform satisfactorily if any one or more of its components or modes of operation is functioning satisfactorily; the entire system would fail only if all its components or modes of operation fail.
In the framework of load-resistance interference for different modes of operation, the failure probability of a parallel system, according to Eq. (7.9), is

|
|||||||||||
|
|
|
|
|
|
||||||

which can be computed as the multivariate normal probability discussed in Sec. 2.7.2. The bounds for system failure probability also can be computed if the exact value of Pf, sys is not required. In the case that all performance variables W’s are independent, the system failure probability reduces to
M
Pf, sys = П ®(-Pm) (7.44)
m=1
Alternatively, the reliability of a parallel system can be expressed as
The second-order bounds for this system reliability, according to Eq. (7.27), are
in which L( jij, em 1 pjm) — P [Zj > ej, Zm > em — Ф( ej, em 1 pjm) +
Ф(в j) + Ф^)-!.
Example 7.8 Referring to Example 7.6, determine the system reliability by considering that the system would fail if all three modes of operation fail.
Solution Since the system is in parallel, the system failure probability can be calculated as
Pf, sys — P(Wi < 0, W2 < 0, W3 < 0)
— P(Z1 < -2.68, Z2 < -3.46, Z3 < -2.68) — 0.0001556
which is obtained in Example 7.6. Hence the reliability of the system is 0.9998444.
In the framework of time-to-failure analysis, the unreliability of a parallel system involving M independent components can be computed as
M
![]() pf, sys(t) — ^ pf, m(t)
pf, sys(t) — ^ pf, m(t)
m—1
in which pf, m(t) — P(Tm < t), the unreliability of the mth component within the specified time interval (0, t]. Hence the system reliability in time interval (0, t] is
M
Ps, sys(t) = 1 – Pf, sys(t) = 1 – П Pf, m(t) (7.48)
m=l
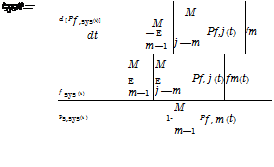 |
||
The failure density function f sys(t) and failure rate hsys(t) for a parallel system consisting of M independent components are
For each component having an exponential failure density function with the parameter Xm, for m — 1,2,…, M, the failure probability of a parallel system can be computed as
M
Pf ,sys(t) — П (1 – e~lmt) (7.51)
m—1
with the corresponding system reliability
M
Ps, sys(t) — 1 – П (1 – e-lmt) (7.52)
m—1
The system failure density function f sys(t) is
In the case that all components have an identical failure rate, that is, X1 — X2 — ■ ■ — XM — X, the MTTF of the system is
The unavailability of a parallel system involving M independent components is
M
Usys(t) —Ц Um(t) (7.55a)
m—1
and the corresponding system availability is
M
Asys(t) = 1 – Ц Um(t) (7.55b)
m=1
Under the condition of independent exponential repair functions for the M components, the unavailability of a parallel system is
and the stationary system unavailability is
Example 7.9 As an example of a parallel system, consider a pumping station consisting of two identical pumps operating in a redundant configuration so that either pump could fail, and the peak discharge could still be delivered. Both pumps have a failure rate of k = 0.0005 failures/h, and both pumps start operating at t = 0. The system reliability for a mission time of t = 1000 h, according to Eq. (7.52), is
![]()
ps, sys(t = 1000) = 1 – (1 – e-(0 0005>(1000>)(1 – e-(0-0005)(1000)) = 0.8452 The MTTF, according to Eq. (7.53), is






Leave a reply