Overall summary of AFOSM reliability method
Convergence criteria for locating the design point. The previously described Hasofer-Lind and Ang-Tang iterative algorithms to determine the design point indicate that the iterations may end when x(r) and x(r+1> are sufficiently close. The key question then becomes what constitutes sufficiently close. In the examples given previously in this section, the iterations were stopped when the
difference between the current and previous design point was less than 0.001. Whereas such a tight tolerance worked for the pipe-capacity examples in this book, it might not be appropriate for other cases, particularly for practical problems. Thus alternative convergence criteria often have been used.
In some cases, the solution has been considered to have converged when the values of в(г) and віт+1) are sufficiently close. For example, Ang and Tang (1984, pp. 361-383) presented eight example applications of the AFOSM method to civil engineering systems, and the convergence criteria for differences in в ranged from 0.025 to 0.001. The Construction Industry Research and Information Association (CIRIA, 1977) developed an iterative approach similar to that of Ang and Tang (1984), only their convergence criterion was that the performance function should equal zero within some tolerance. The CIRIA procedure was applied in the uncertainty analysis of backwater computations using the HEC-2 water surface profiles model done by Singh and Melching (1993).
In order for iterative algorithms to locate the design point to achieve convergence, the performance function must be locally differentiable, and the original density functions of Xk must be continuous and monotonic, at least for Xk < xk* (Yen et al., 1986). If the performance function is discontinuous, it must be treated as a series of continuous functions.
The search for the design point may become numerically more complex if the performance function has several local minima or if the original density functions of the Xk are discontinuous and bounded. It has been found that some of the following problems occasionally may result for the iteration algorithms to locate the design point (Yen et al., 1986):
1. The iteration may diverge or it may give different в values because of local minima in the performance function.
2. The iteration may converge very slowly when the probability of failure is very small, for example, pf < 10-4.
3. In the case of bounded random variables, the iteration may yield some xk* values outside the bounded range of the original density function. However, if the bounds are strictly enforced, the iterations may diverge.
Yen et al. (1986) recommended use of the generalized reduced gradient (GRG) optimization method proposed by Cheng et al. (1982) to determine the design point to reduce these numerical problems. However, the GRG-based method may not work well when complex computer models are needed to determine the system performance function.
Melching (1992) applied the AFOSM method using the Rackwitz iterative algorithm (Rackwitz and Fiessler, 1978), which is similar to the Ang-Tang algorithm, to determine the design point for estimation of the probability of flooding for 16 storms on an example watershed using two rainfall-runoff models. In this application, problems with performance function discontinuities, slow convergence for small values of pf, and divergence in the estimated в values were experienced for some of the cases. In the case of discontinuity in the performance function (resulting from the use of a simple initial loss – continuing loss rate abstraction scheme), in some cases the iterations went back and forth between one side of the discontinuity and the other, and convergence in the values of the xk s could not be achieved. Generally, in such cases, the value of в had converged to the second decimal place, and thus a good approximation of в* corresponding to the design point was obtained.
For extreme probability cases (в > 2.5), the iterations often diverged. The difference in в values for performance function values near zero typically was on the order of 0.2 to 0.4. The iteration of which the в value was smallest was selected as a reasonable estimate of the true в* corresponding to the design point. In Melching (1992), the pf values so approximated were on the order of 0.006 to 0.00004. Thus, from a practical viewpoint of whether or not a flood is likely, such approximations of в* do not greatly change the estimated flood risk for the event in question. However, ifvarious flood-mitigation alternatives were being compared in this way, one would have to be very careful that consistent results were obtained when comparing the alternatives.
A shortcoming of the afosm reliability index. As shown previously, use of the
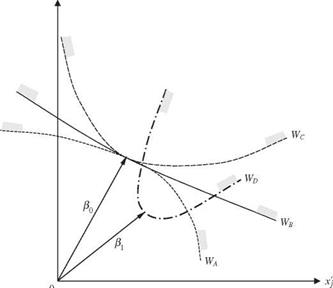
AFOSM reliability index removes the problem of lack of invariance associated with the MFOSM reliability index. This allows one to place different designs on the same common ground for comparing their relative reliabilities using в-AF^M. A design with higher value of влгозм would be associated with a higher reliability and lower failure probability. Referring to Fig. 4.14, in which failure surfaces of four different designs are depicted in the uncorrelated standardized parameter space, an erroneous conclusion would be made if one assesses the relative reliability on the basis of the reliability index. Note that in Fig. 4.14 the designs A, B, and C have identical values of the reliability index, but the size of their safe regions SA, SB, and SC are not the same, and in fact, they satisfy SA c SB c SC. The actual reliability relationship among the three designs should be ps(A) < ps(B) < ps(C), which is not reflected by the reliability index. One could observe that if the curvatures of different failure surfaces at the design point are similar, such as those with designs A and B, relative reliabilities between different designs could be indicated accurately by the value of reliability index. On the other hand, when the curvatures offailure surfaces are significantly different, such as those for designs C and D, вAFOsM alone could not be used as the basis for comparison.
For this reason, Ditlevsen (1979) proposed a generalized reliability index во = Ф(у), with y being a reliability measure obtained from integrating a weight function over the safe region S, that is,
Y = Ф (x) d x (4.83)
J x es
in which ф (x) is the weight function, which is rotationally symmetric and positive (Ditlevsen, 1979). One such function that is mathematically tractable is
|
xk
Figure 4.14 Nonunique reliability associated with an identical reliability index. |
the K-dimensional standardized independent normal PDF. Although the generalized reliability index provides a more consistent and selective measure of reliability than ^atosm for a nonlinear failure surface, it is, however, more computationally difficult to obtain. From a practical viewpoint, most engineering applications result in the general reliability index whose value is close to eAFoSM. Only in cases where the curvature of the failure surface at the design point is large and there are several design points on the failure surface would the two reliability indices deviate significantly.






Leave a reply