Multivariate normal distributions

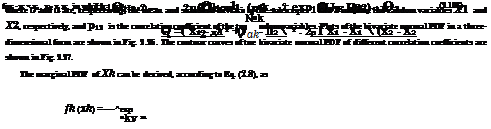A bivariate normal distribution has a PDF defined as

for k = 1 and 2. As can be seen, the two random variables having a bivariate normal PDF are, individually, normal random variables. It should be pointed out that given two normal marginal PDFs, one can construct a bivariate PDF that is not in the form of a bivariate normal as defined by Eq. (2.108).

According to Eq. (2.17), the conditional normal PDF of X11 x2 can be ob­tained as

(2.109)
>■;

.H.

0.1

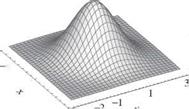
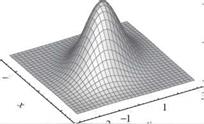
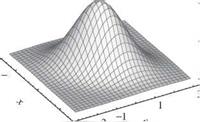
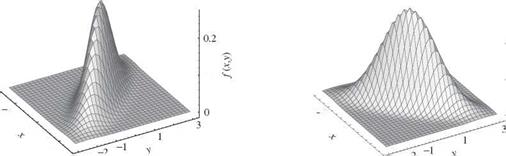
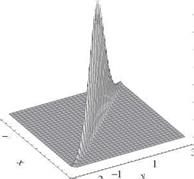
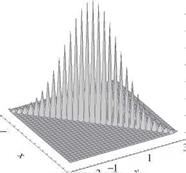Figure 2.26 Three-dimensional plots of bivariate standard normal probability density functions. (After Johnson and Kotz, 1976.)

O1 > O2 Oj = O2 O1 < O2

x2

в = 135° XJ

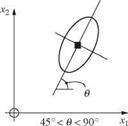
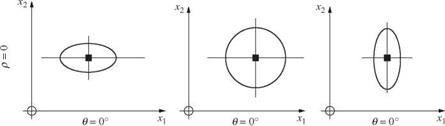
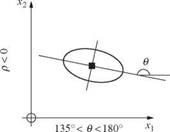
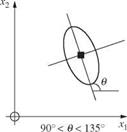
Figure 2.27 Contour of equal density of bivariate standard normal probability density func­tions. (After Johnson and Kotz, 1976.)

for —to < x1 < to. Based on Eq. (2.109), the conditional expectation and variance of the normal random variable X11 x2 can be obtained as

E(X1 | x2) = P1 + P12(ff1/V2)(x2 – P2) (2.110)

Var(X11 x2) = (1 – P22) (2.111)

Expressions of the conditional PDF, expectation, and variance for X2 | x1 can be obtained immediately by exchanging the subscripts in Eqs. (2.109) through (2.111).

For the general case involving K correlated normal random variables, the multivariate normal PDF is

in which і, = (д1, p.2,…, /гК )t, a К x 1 column vector of the mean values of the variables, with the superscript t indicating the transpose of a matrix or vector, and Cx is a К x К covariance matrix:

^11	012	■ ‘ ‘ p1K
021	022	■ ■ ■ 02K
Pk 1	pK 2	■ ■ ■ °KK_

Cov(X) = С, =

This covariance matrix is symmetric, that is, Pjk = okj, for j = k, where ajk = Cov(Xj, Xk). In matrix notation, the covariance matrix for a vector of random variables can be expressed as

С, = E [(X — і,)(X — і,)4

In terms of standard normal random variables, Zk = (Xk — ik)’ak, the stan­dardized multivariate normal PDF, can be expressed as

in which Rx = Cz = E (ZZ *) is a К x К correlation matrix:

1	P12 ■	■ P1K
P21	1 ■	■ P2K
PK1	PK2 ■	■ 1

Corr(X) = Cov(Z) = Rx =

with pjk = Cov(Zj, Zk) being the correlation coefficient between each pair of normal random variables Xj and Xk. For bivariate standard normal variables,

the following relationships of cross-product moments are useful (Hutchinson and Lai, 1990):

for m and n being positive integer numbers.