Generation of Univariate Random Numbers for Some Distributions

Hydrosystems Engineering Reliability Assessment and Risk Analysis

This section briefly outlines efficient algorithms for generating random variates for some probability distributions commonly used in hydrosystems engineering and analysis.

6.1.2 Normal distribution

A normal random variable with a mean цx and standard deviation ox, denoted as X ~ N(p. x, ox), has a PDF given in Eq. (2.58). The relationship between X and the standardized normal variable Z is

X = ^x + OxZ (6.11)

in which Z is the standard normal random variable having a mean 0 and unit standard deviation, denoted as Z ~ N(0,1). Based on Eq. (6.11), normal ran­dom variates with a specified mean and standard deviation can be generated from standard normal variates. Herein, three simple algorithms for generating standard normal variates are described.

Box-Muller algorithm. The algorithm (Box and Muller, 1958) produces a pair of independent N(0,1) variates as

z1 = v/-2ln(u1) cos(2n u2)

______________ (6.12)

Z2 = /-2ln(U2) sin(2nU2)

in which u1 and u2 are independent uniform variates from U(0,1). The algo­rithm involves the following steps:

1. Generate two independent uniform random variates u1 and u2 from U(0, 1).

2. Compute z1 and z2 simultaneously using u1 and u2 according to Eq. (6.12).

Marsagalia-Bray algorithm. Marsagalia and Bray (1964) proposed an alternative algorithm that avoids using trigonometric evaluations. In their algorithm, two independent uniform random variates u1 and u2 are produced to evaluate the following three expressions:

V1 = 2U1 — 1

V2 = 2U2 — 1 (6.13)

R = V1 + V 22

If R > 1, the pair (u1, u2) is rejected from further consideration, and a new pair (u1, u2) is generated. For the accepted pair, the corresponding standard

Подпись: Zi = V і Подпись: -2ln( R) R Подпись: Z2 = V 2 Подпись: -2ln( R) R Подпись: (6.14)

Подпись: (6.15) (6.16) Подпись:

Подпись: The Marsagalia-Bray algorithm involves the following steps: 1. Generate two independent uniform random variates u1 and u2 from U(0, 1). 2. Compute V1, V2, and R according to Eq. (6.13). 3. Check if R < 1. If it is true, compute the two corresponding N(0, 1) variates using Eq. (6.14). Otherwise, reject (u1, u2) and return to step 1. Algorithm based on the central limit theorem. This algorithm is based on the central limit theorem, which states that the sum ofindependent random variables approaches a normal distribution as the number ofrandom variables increases. Specifically, consider the sum of J independent standard uniform random variates from U(0, 1). The following relationships are true:
Подпись: *( £J V" feUj)=J
Подпись: By the central limit theorem, this sum of J independent U’s would approach a normal distribution with the mean and variance given in Eqs. (6.15) and (6.16), respectively. Constrained by the unit variance of the standard normal variates, Eq. (6.16) yields J = 12. Then a standard normal variate is generated by
Подпись: (6.17)
Подпись: j=1
Подпись: The central limit theorem-based algorithm can be implemented as 1. Generate 12 uniform random variates from U(0, 1). 2. Compute the corresponding standard normal variate by Eq. (6.17). There are many other efficient algorithms developed for generating normal random variates using the variable transformation method and AR method. For these algorithms readers are referred to Rubinstein (1981).

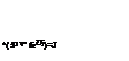normal variates are computed by



Related Posts:

Updated: 20 ноября, 2015 — 4:14 дп