Procedures described in Sec. 6.5.2 are for generating multivariate normal (Gaussian) random variables without imposing constraints or restriction on the values of variates. The procedures under this category are also called unconditional (or nonconditional) simulation (Borgman and Faucette, 1993; Chiles and Delfiner, 1999). In hydrosystems modeling, random variables often exist for which, in addition to their statistical correlation, they are physically related in certain functional forms. In particular, this section describes the procedures for generating multivariate Gaussian random variates that must satisfy prescribed linear relationships. An example is the use of unit hydrograph model for estimating design runoff based on a design rainfall excess hyetograph. The unit hydrograph is applied as follows:
Pu= q (6.38)
where P is an n x J Toeplitz matrix defining the design effective rainfall hyetograph, u is a J x 1 column vector of unit hydrograph ordinates, and q is the n x 1 column vector of direct runoff hydrograph ordinates. In the process of deriving a unit hydrograph for a watershed, there exist various uncertainties rendering u uncertain. Hence the design runoff hydrograph q obtained from Eq. (6.38) is subject to uncertainty. Therefore, to generate a plausible direct runoff hydrograph for a design rainfall excess hyetograph, one could generate unit hydrographs that must consider the following physical constraint:
J
Y^Uj = c (6.39)
j=1
in which c is a constant to ensure that the volume of unit the hydrograph is one unit of effective rainfall.
The linearly constrained Monte Carlo simulation can be conducted by using the acceptance-rejection method first proposed by von Neumann (1951). The AR method generally requires a large number of simulations to satisfy
the constraint and, therefore, is not computationally efficient. Borgman and Faucettee (1993) developed a practical method to convert a Gaussian linearly constrained simulation into a Gaussian conditional simulation that can be implemented straightforwardly. The following discussions will concentrate on the method of Borgman and Faucette (1993).
 |
 |
 |
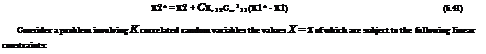Conditional simulation (CS) was developed in the field of geostatistics for modeling spatial uncertainty to generate a plausible random field that honors the actual observational values at the sample points (Chiles and Delfiner, 1999). In other words, conditional simulation yields special subsets of realizations from an unconditional simulation in that the generated random variates match with the observations at the sample points. For the multivariate normal case, the Gaussian conditional simulation is to simulate a normal random vector X2 conditional on the normal random vector X1 = x1*. To implement the conditional simulation, define a new random vector X encompassing of Xi and X2 as
generated conditioned on y1 = b. Hence, using the spectral decomposition described in Sec. 6.5.2.2, random vector X subject to linear constraints Eq. (6.42) can be obtained in the following two steps:
1. Calculate (m + K)-dimensional multivariate normal random vector y by unconditional simulation as
У = (yO = VyA-°y5 Z + Ъ (6.45)
where y1 is an m x 1 column vector, y2 is a K x 1 column vector; Vy is an (m + K) x (m + K) eigenvector matrix of Cy, and Лу is a diagonal matrix of eigenvalues of Cy, and Z’ is an (m + K) column vector of independent standard normal variates.
2. Calculate the linearly constrained K-dimensional vector of random variates x, according to Eq. (6.41), as
x = y2* = y2 + C y,12C-,n(b — y1) (6.46)
This constrained multivariate normal simulation has been applied, by considering the uncertainties in the unit hydrograph and geomorphologic instantaneous unit hydrograph, to reliability analysis of hydrosystems engineering infrastructures (Zhao et al., 1997a, 1997b; Wang and Tung, 2005).
