Gamma distribution and variations

The gamma distribution is a versatile continuous distribution associated with a positive-valued random variable. The two-parameter gamma distribution has
a PDF defined as

f g(x | а, в) = 1 (x/в)а—1 ex/fl for x > 0 (2.72)

вГ(а)

in which в > 0 and а > 0 are the parameters and Г(») is a gamma function defined as

ta-1e-t dt
Г(а)	(2.73)
0

The mean, variance, and skewness coefficient of a gamma random variable having a PDF as Eq. (2.72) are

gx = A.1 = ав = ав2 Yx = 2/ja (2.74)

In terms of L-moments, the second-order L-moment is

вГ(а + 0.5)

^2 = ,—r( s

(а)

where f is the lower bound. The two-parameter gamma distribution can be reduced to a simpler form by letting Y = X/в, and the resulting one-parameter gamma PDF (called the standard gamma distribution) is

f g(y | а) = —Цya V for y > 0 Г(а)

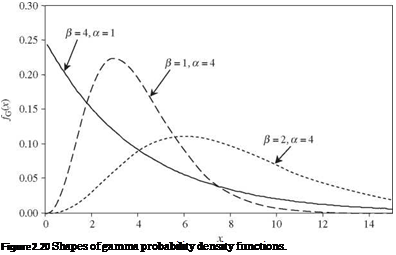
Tables of the cumulative probability of the standard gamma distribution can be found in Dudewicz (1976). Shapes of some gamma distributions are shown in Fig. 2.20 to illustrate its versatility. If а is a positive integer in Eq. (2.78), the distribution is called an Erlang distribution.

When а = 1, the two-parameter gamma distribution reduces to an exponential distribution with the PDF

f EXp(x | в) = e х/в/в for x > 0 (2.79)

An exponential random variable with a PDF as Eq. (2.79) has the mean and standard deviation equal to в (see Example 2.8). Therefore, the coefficient of

variation of an exponential random variable is equal to unity. The exponential distribution is used commonly for describing the life span of various electronic and mechanical components. It plays an important role in reliability mathe­matics using time-to-failure analysis (see Chap. 5).

Two variations of the gamma distribution are used frequently in hydrologic frequency analysis, namely, the Pearson and log-Pearson type 3 distributions. In particular, the log-Pearson type 3 distribution is recommended for use by the U. S. Water Resources Council (1982) as the standard distribution for flood frequency analysis. A Pearson type 3 random variable has the PDF

‘"’x"*,"-о)-ЩО) (it)w,2-80’

with a > 0, x > * when ft > 0 and with a > 0, x < * when ft < 0. When ft > 0, the Pearson type 3 distribution is identical to the three-parameter gamma distribution. However, the Pearson type 3 distribution has the flexibility to model negatively skewed random variables corresponding to ft < 0. Therefore, the skewness coefficient of the Pearson type 3 distribution can be computed, from modifying Eq. (2.74), as sign(^)2Д/а.

Similar to the normal and lognormal relationships, the PDF of a log-Pearson type 3 random variable is

with a > 0, x > e* when ft > 0 and with a > 0, x < e* when ft < 0. Numerous studies can be found in the literature about Pearson type 3 and log-Pearson

type 3 distributions. Kite (1977), Stedinger et al. (1993), and Rao and Hamed (2000) provide good summaries of these two distributions.

Evaluation of the probability of gamma random variables involves computa­tions of the gamma function, which can be made by using the following recursive formula:

r(a) = (a — 1)r(a — 1) (2.82)

When the argument a is an integer number, then Г(а) = (a — 1)! = (a — 1)(a — 2) • •• 1. However, when a is a real number, the recursive relation would lead to r(a;) as the smallest term, with 1 < a’ < 2. The value of T(a7) can be determined by a table of the gamma function or by numerical integration on Eq. (2.73). Al­ternatively, the following approximation could be applied to accurately estimate the value of r(a;) (Abramowitz and Stegun, 1972):

5

r(a;) = Г(x + 1) = 1 + ^ aixl for 0 < x < 1 (2.83)

i = 1

in which a1 = -0.577191652, a2 = 0.988205891, a3 = -0.897056937, a4 = 0.4245549, and a5 = — 0.1010678. The maximum absolute error associated with Eq. (2.83) is 5 x 10-5.