Failure rate and hazard function

The failure rate is defined as the number of failures occurring per unit time in a time interval (t, t + At ] per unit of the remaining population in operation at

TABLE 5.1 Selected Time-to-Failure Probability Distributions and Their Properties

time t. Consider that a system consists of N identical components. The number of failed components in (t, t + At ], NF (At), is

NF ( At) = N x pf (t + At) — N x pf (t) = N [pf (t + At) — pf (t)]

and the remaining number of operational components at time t is

N(t) = N x ps(t)

Then, according to the preceding definition of the failure rate, the instantaneous failure rate h(t) can be obtained as

h(t) = limA<^0	‘Nf (At )/A t	= limA<^0	N x pf (t + At) — N x pf (t)"
[ N (t) J	N(t) x At
= —^lim ps(t)	"pf (t + At) — pf (t) At^0 A. At

1 d [pf (t)] ps(t) dt ft (t) ps(t)

(5.3)

This instantaneous failure rate is also called the hazard function or force-of — mortality function (Pieruschka, 1963). Therefore, the hazard function indicates the change in the failure rate over the operating life of a component. The

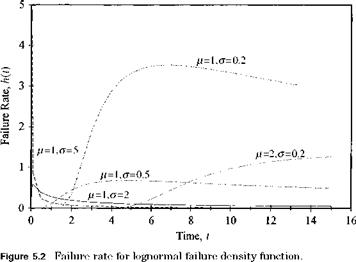
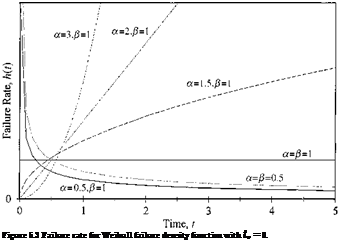
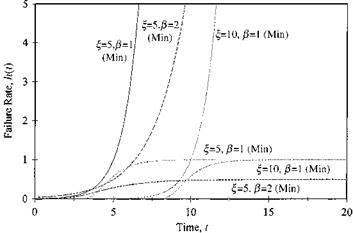
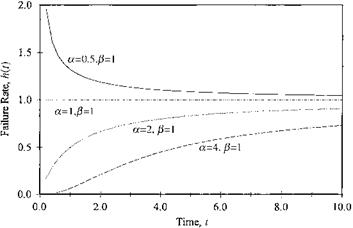
hazard functions for some commonly used failure density functions are given in Table 5.1. Figures 5.2 through 5.6 show the failure rates with respect to time for various failure density functions.

Alternatively, the meaning of the hazard function can be seen from

in which the term [pf (t + At) — pf (t)]/ps(t) is the conditional failure proba­bility in (t, t + At], given that the system has survived up to time t. Hence the

Figure 5.4 Failure rate for Gumbel failure density function.

hazard function can be interpreted as the time rate of change of the condi­tional failure probability for a system given that has survived up to time t. It is important to differentiate the meanings of the two quantities ft (t) dt and h(t) dt, with the former representing the probability that a component would experience failure during the time interval (t, t + dt]—it is unconditional— whereas the latter, h(t) dt, is the probability that a component would fail dur­ing the time interval (t, t + At]—conditional on the fact that the component has been in an operational state up to time instant t.

Figure 5.5 Failure rate for two-parameter gamma failure density function.

Figure 5.6 Failure rate for uniform failure density function.