For a chosen distributional model, its shape and position are completely defined by the associated parameters. By referring to Eq. (3.5), determination of the quantile also requires knowing the values of the parameters в.
There are several methods for estimating the parameters of a distribution model on the basis of available data. In frequency analysis, the commonly used parameter-estimation procedures are the method of maximum likelihood and the methods of moments (Kite, 1988; Haan, 1977). Other methods, such as method of maximum entropy (Li et al., 1986), have been applied.
3.6.1 Maximum-likelihood (ML) method
This method determines the values of parameters of a distribution model that maximizes the likelihood of the sample data at hand. For a sample of n independent random observations, x = (x1, x2,…, xn)1, from an identical distribution, that is,
Xi ~ fx(x | в) for i = 1,2,…, n
in which в = (0i, 02,…, 6m) a vector of m distribution model parameters, the likelihood of occurrence of the samples is equal to the joint probability
of {xi}i=1,2,…,n calculable by
n
L(x | в) = Ц fx(xi | в) (3.10)
i=1
in which L(x |в) is called the likelihood function. The ML method determines the distribution parameters by solving
Max L(x | в) = maxln[L(x | в)]
в в
or more specifically
nn
Maxll fx(Xi | в) = ln[fx(Xi | в)]
i=1 i=1
 |
 |
 |
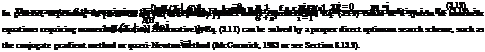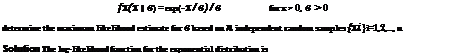As can be seen, solving for distribution-model parameters by the ML principle is an unconstrained optimization problem. The unknown model parameters can be obtained by solving the following necessary conditions for the maximum:
 |
which is the sample mean.
 |
 |
 |
 |
Example 3.5 Consider a set of n independent samples, x = (xi, x%,…, xn)1, from a normal distribution with the following PDF:
Determine the ML estimators for the parameters a and в.
 |
 |
 |
Solution The likelihood function for the n independent normal samples is
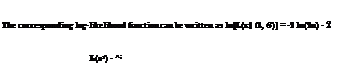n, Y^n=1(xi — a)2
2в2
 |
 |
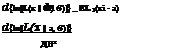Taking the partial derivatives of the preceding log-likelihood function with respect to a and в2 and setting them equal to zero results in
After some algebraic manipulations, one can easily obtain the ML estimates of normal distribution parameters a and в as
a Ei=1 xi в2 Ei=1(xi — a)2
aML = —n~ ^L =——————- n————
As can be seen, the ML estimation of the normal parameters for a is the sample mean and for в2 is a biased variance.
3.6.2 Product-moments-based method
By the moment-based parameter-estimation methods, parameters of a distribution are related to the statistical moments of the random variable. The conventional method of moments uses the product moments of the random variable. Example 3.3 for frequency analysis is typical of this approach. When sample data are available, sample product moments are used to solve for the model parameters. The main concern with the use of product moments is that their reliabilities owing to sampling errors deteriorate rapidly as the order of moment
increases, especially when sample size is small (see Sec. 3.1), which is often the case in many geophysical applications. Hence, in practice only, the first few statistical moments are used. Relationships between product-moments and parameters of distribution models commonly used in frequency analysis are listed in Table 3.4.
As described in Sec. 2.4.1, the L-moments are linear combinations of order statistics (Hosking, 1986). In theory, the estimators of L-moments are less sensitive to the presence of outliers in the sample and hence are more robust than the conventional product moments. Furthermore, estimators of L-moments are less biased and approach the asymptotic normal distributions more rapidly and closely. Hosking (1986) shows that parameter estimates from the L-moments are sometimes more accurate in small samples than are the maximum — likelihood estimates.
To calculate sample L-moments, one can refer to the probability-weighted moments as
вr = M1,r, o = E{X[Fx(X)]r} for r = 0,1,… (3.13)
which is defined on the basis of nonexceedance probability or CDF. The estimation of вг then is hinged on how Fx(X) is estimated on the basis of sample data.
Consider n independent samples arranged in ascending order as X(n) < X(n-1) < ■ ■ ■ < X(2) < X(1). The estimator for Fx(X(m>) for the mth — order statistic can use an appropriate plotting-position formula as shown in Table 3.2, that is,
m ___ a
F( X (m)) = 1———————- —— T for m = 1,2,…, n
n + 1 — b
with а > 0 and b > 0. The Weibull plotting-position formula (a = 0, b = 0) is a probability-unbiased estimator of Fx(X(m>). Hosking et al. (1985a, 1985b) show that a smaller mean square error in the quantile estimate can be achieved by using a biased plotting-position formula with a = 0.35 and b = 1. According to the definition of the в-moment вг in Eq. (3.13), its sample estimate br can be obtained easily as
1n
br = — J^X(m)[F (X(m))]r for Г = 0,1, … (3.14)
П i=1
Stedinger et al. (1993) recommend the use of the quantile-unbiased estimator of Fx(X(m)) for calculating the L-moment ratios in at-site and regional frequency analyses.
|
 |
|
|
|
||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
 |
||||||||
|
|
|
||||||
|
||||||||
 |
||||||||
|
|
|||||||
|
||||||||
|
||||||||
 |
||||||||
|
|
|||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
|
|||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
|
||||||||
 |
||||||||
 |
||||||||
|
||||||||
|
||||||||
 |
||||||||
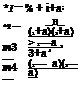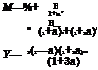For any distribution, the L-moments can be expressed in terms of the probability-weighted moments as shown in Eq. (2.28). To compute the sample L-moments, the sample probability-weighted moments can be obtained as
11 = 60
12 = 261 — 60
13 = 662 — 661 + 60 (3.15)
14 = 2063 — 3062 + 1261 — 60
 |
 |
 |
 |
where the lr s are sample estimates of the corresponding L-moments, the Xr s, respectively. Accordingly, the sample L-moment ratios can be computed as
where t2, t3, and t4 are the sample L-coefficient of variation, L-skewness coefficient, and L-kurtosis, respectively. Relationships between L-moments and parameters of distribution models commonly used in frequency analysis are shown in the last column of Table 3.4.
Example 3.6 Referring to Example 3.3, estimate the parameters of a generalized Pareto (GPA) distribution by the L-moment method.
Solution Since the GPA is a three-parameter distribution, the calculation of the first three sample L-moments is shown in the following table:
|
Year |
qi (ft3/s) |
Ordered q(i) (ft3/s) |
Rank (i) |
F (q(i)) = (i — 0.35)/n |
q(i) x F(q(i)) |
q(i) x F (q(i))2 |
q(i) x F (q(i))3 |
|
1961 |
390 |
342 |
1 |
0.0433 |
14.82 |
0.642 |
0.0278 |
|
1962 |
374 |
374 |
2 |
0.1100 |
41.14 |
4.525 |
0.4978 |
|
1963 |
342 |
390 |
3 |
0.1767 |
68.90 |
12.172 |
2.1504 |
|
1964 |
507 |
414 |
4 |
0.2433 |
100.74 |
24.513 |
5.9649 |
|
1965 |
596 |
416 |
5 |
0.3100 |
128.96 |
39.978 |
12.3931 |
|
1966 |
416 |
447 |
6 |
0.3767 |
168.37 |
63.419 |
23.8880 |
|
1967 |
533 |
505 |
7 |
0.4433 |
223.88 |
99.255 |
44.0030 |
|
1968 |
505 |
505 |
8 |
0.5100 |
257.55 |
131.351 |
66.9888 |
|
1969 |
549 |
507 |
9 |
0.5767 |
292.37 |
168.600 |
97.2260 |
|
1970 |
414 |
524 |
10 |
0.6433 |
337.11 |
216.872 |
139.5210 |
|
1971 |
524 |
533 |
11 |
0.7100 |
378.43 |
268.685 |
190.7666 |
|
1972 |
505 |
543 |
12 |
0.7767 |
421.73 |
327.544 |
254.3922 |
|
1973 |
447 |
549 |
13 |
0.8433 |
462.99 |
390.455 |
329.2836 |
|
1974 |
543 |
591 |
14 |
0.9100 |
537.81 |
489.407 |
445.3605 |
|
1975 |
591 |
596 |
15 |
0.9767 |
582.09 |
568.511 |
555.2459 |
|
Sum = |
7236 |
4016.89 |
2805.930 |
2167.710 |
Note that the plotting-position formula used in the preceding calculation is that proposed by Hosking et al. (1985a) with a = 0.35 and b = 1.
Based on Eq. (3.14), the sample estimates of Pj, for j = 0,1, 2, 3, are Ьз = 428.4, b1 = 267.80, Ьз = 187.06, and b4 = 144.51. Hence, by Eq. (3.15), the sample estimates of к j, j = 1,2, 3,4, are I1 = 482.40, I2 = 53.19, I3 = -1.99, and I4 = 9.53, and the corresponding sample L-moment ratios Tj, for j = 2, 3, 4, are t2 = 0.110, t3 = —0.037, and t4 = 0.179.
 |
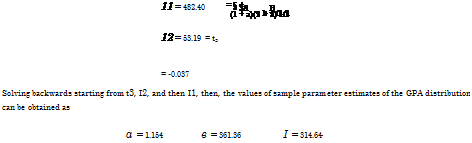By referring to Table 3.4, the preceding sample h = 482.40, I2 = 53.19, and t3 = —0.037 can be used in the corresponding L-moment and parameter relations, that is,
