Determinations of Availability and Unavailability
A repairable system experiences a repetition of the repair-to-failure and failure – to-repair processes during its service life. Hence the probability that a system is in an operating condition at any given time t for a repairable system is different from that for a nonrepairable system. The term availability A(t) generally is
used for repairable systems to indicate the probability that the system is in an operating condition at any given time t. It also can be interpreted as the percentage of time that the system is in an operating condition within a specified time period. On the other hand, reliability ps(t) is appropriate for nonrepairable systems, indicating the probability that the system has been continuously in an operating state starting from time zero up to time t.
There are three types of availability (Kraus, 1988). Inherent availability is the probability of a system, when used under stated conditions and without consideration of any scheduled or preventive actions, in an ideal support environment, operating satisfactorily at a given time. It does not include ready time, preventive downtime, logistic time, and administrative time. Achieved availability considers preventive and corrective downtime and maintenance time. However, it does not include logistic time and administrative time. Operational availability considers the actual operating environment. In general, the inherent availability is higher than the achieved availability, followed by the operational availability (see Example 5.13). Of interest to design is the inherent availability; this is the type of availability discussed in this chapter.
In general, the availability and reliability of a system satisfy the following inequality relationship:
0 < ps(t) < A(t) < 1 (5.40)
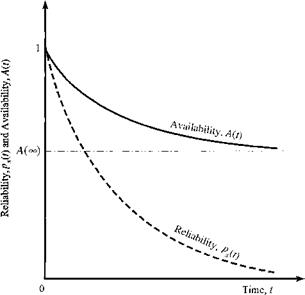
with the equality for ps(t) and A(t) holding for nonrepairable systems. The reliability of a system decreases monotonically to zero as the system ages, whereas the availability of a repairable system decreases but converges to a positive probability (Fig. 5.16).
|
Figure 5.16 Comparison of reliability and availability. |
The complement to the availability is the unavailability U(t), which is the probability that a system is in a failed condition at time t, given that it was in an operating condition at time zero. In other words, unavailability is the percentage of time the system is not available for the intended service in time period (0, t], given that it was operational at time zero. Availability, unavailability, and unreliability satisfy the following relationships:
A(t) + U (t) = 1 (5.41)
0 < U(t) < pf (t) < 1 (5.42)
For a nonrepairable system, the unavailability is equal to the unreliability, that
is, U(t) = pf (t).
Recall the failure rate in Sec. 5.2.2 as being the probability that a system experiences a failure per unit time at time t, given that the system was operational at time zero and has been in operation continuously up to time t. This notion is appropriate for nonrepairable systems. For a repairable system, the term conditional failure intensity p(t) is used, which is defined as the probability that the system will fail per unit time at time t, given that the system was operational at time zero and also was in an operational state at time t. Therefore, the quantity p(t) dt is the probability that the system fails during the time interval (t, t + dt], given that the system was as good as new at time zero and was in an operating condition at time t. Both p(t) dt and h(t) dt are probabilities that the system fails during the time interval (t, t + dt], being conditional on the fact that the system was operational at time zero. The difference is that the latter, h(t) dt, requires that the system has been in a continuously operating state from time zero to time t, whereas the former allows possible failures before time t, and the system is repaired to the operating state at time t. Hence p(t) = h(t) for the general case, and they are equal for nonrepairable systems or when h(t) is a constant (Henley and Kumamoto, 1981).
A related term is the unconditional failure intensity w(t), which is defined as the probability that a system will fail per unit time at time t, given that the system is in an operating condition at time zero. Note that the unconditional failure intensity does not require that the system is operational at time t. For a nonrepairable system, the unconditional failure intensity is equal to the failure density ft (t). The number of failures experienced by the system within a specified time interval [t1, t2] can be evaluated as
W(tb t2) =f 2 w(t) dr (5.43)
t1
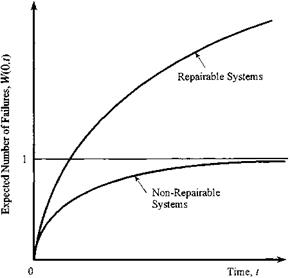
Hence, for a nonrepairable system, W(0, t) is equal to the unreliability, which approaches unity as t increases. However, for repairable systems, W(0, t) would diverge to infinite as t gets larger (Fig. 5.17).
On the repair aspect of the system, there are elements similar to those of the failure aspect. The conditional repair intensity p(t) is defined as the probability that a system is repaired per unit time at time t, given that the system was in
|
Figure 5.17 Expected number of failures for repairable and nonrepairable systems. |
an operational state initially at time zero but in a failed condition at time t. The unconditional repair intensity y(t) is the probability that a failed system will be repaired per unit time at time t, given that it was initially in an operating condition at time zero. The number of repairs over a specified time period (ti, t2), analogous to Eq. (5.43), can be expressed as
r(ti, t2) = [ y(r)dr (5.44)
Jt1
in which Г(0, t) is the expected number of repairs for a repairable system within the time interval [t1, t2]. A repairable system has Г(0, t) approaching infinity as t increases, whereas it is equal to zero for a nonrepairable system. It will be shown in the next subsection that the difference between W(0, t) and Г(0, t) is the unavailability U(t).






Leave a reply