Determination of bounds on multivariate normal probability

Instead of computing the exact value of Ф(z |Rx), several methods have been proposed to determine the bounds on the exact value of Ф(z |Rx). This section describes three such bounds.

Bounds of Rackwitz. The scheme of Rackwitz (1978) is based on the decompo­sition of a positive correlation coefficient pij = XiXj, for i, j = 1, 2,…, K. The multivariate normal probability Ф(z |Rx) is obtained according to Eq. (2.120). Instead of solving for the exact values for all K(K — 1)/2Xs, Rackwitz selects the smallest three values of z = (z1, z2,…, zK)* in Ф^ |Rx) and solves for the corresponding Xs that satisfy pij = XiXj, for i, j = [1], [2], [3] with subscript [i]
representing the rank of zs in ascending order, that is, Z[p < Z[2] < Z[3] <• ■ ■ < zyK-i] < Z[K]. For example, assume that all ptj s are positive. Based on the three smallest zs, one can solve for X[i] for i = 1, 2, 3 in terms of рщ[j] as

P[1][2] P[1][3] P[2][3]	1/2	P[1][2] P[2][3] P[1][3]	1/2	P[1][3] P[2][3] P[1][2]	1/2
X[1]	X[2]	X[3]

(2.131)

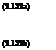For the remaining Xs, their values can be computed as

The upper bound and lower bound of Ф(z |Rx) can be obtained by Eq. (2.120) along with Xs computed by Eqs. (2.132a) and (2.132b), respectively.

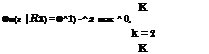Bounds of Ditlevsen. Ditlevsen (1979) proposed an approach for the bounds of the multivariate normal probability as follows:

(2.133b)

in which Фи (z | Rx) and Ф^ | Rx) are the upper and lower bounds of the multi­variate normal probability, respectively, and Ф(zk, Zj | pkj) is the bivariate nor­mal probability. Ditlevsen (1979) further simplified these bounds to involve the evaluation of only the univariate normal probability at the expense of having a more complicated algebraic expression where a narrow bound can be obtained under |p | < 0.6. For a larger correlation coefficient, Ditlevsen (1982) proposed a procedure using conditioning to obtain a narrow bound. The derivations of various probability bounds for system reliability are presented in Sec. 7.2.5

1.00	0.80	0.64	0.51	0.41
0.80	1.00	0.80	0.64	0.51
0.64	0.80	1.00	0.80	0.64
0.51	0.64	0.80	1.00	0.80
0.41	0.51	0.64	0.80	1.00

Example 2.22 Z1, Z2, Z3, Z4, and Z5 are correlated standard normal variables with the following correlation matrix:

Rx —

Determine the multivariate probability P (Zi < -1, Z2 < —2, Z3 < 0, Z4 < 2, Z5 < 1) by Ditlevsen’s approach using the Taylor series expansion. Also compute the bounds for the preceding multivariate normal probability using Rackwitz’s and Ditlevsen’s approaches.

Solution Using Ditlevsen’s Taylor series expansion approach, the initial equicorrela — tion value can be used according to Eq. (2.124) as p = 0.655. The corresponding mul­tivariate normal probability, based on Eq. (2.121), is Ф(г | p = 0.655) = 0.01707. From Eq. (2.122), the first-order error, d Ф(г | p = 0.655), is 0.003958. Results of iterations according to the procedure outlined in Fig. 2.29 are shown below:

i	p	Ф(2|p)	dФ(г|p)
1	0.6550	0.01707	0.3958 x 10—2
2	0.8069	0.02100	—0.1660 x 10—3
3	0.8005	0.02086	—0.3200 x 10—4
4	0.7993	0.02083	—0.5426 x 10—5

At p = 0.7993, the corresponding second-order error term in the Taylor series ex­pansion, according to Eq. (2.126), is

d2Ф(г| p) = 0.01411

Based on Eq. (2.125), the multivariate normal probability can be estimated as Ф(z| Rx) = Ф(г| p = 0.7993) + 0.5d2Ф(г| p = 0.7993)

= 0.02083 + 0.5(0.01411)

0.02789

Using the Rackwitz approach for computing the bounds of the multivariate normal probability, the values ofzs are arranged in ascending order as (гщ, Z[2], Z[3], Z[4], Z[5]) = (—2, —1, 0,1, 2) = (Z2, Z1, Z3, Z5, Z4) with the corresponding correlation matrix as

1.00	0.80	0.80	0.51	0.41
0.80	1.00	0.64	0.41	0.51
0.80	0.64	1.00	0.64	0.80
0.51	0.41	0.80	1.00	0.80
0.64	0.51	0.80	0.80	1.00

R[kj]

The values of ks corresponding to the three smallest zs, that is, —2, —1, and 0, are computed according to Eq. (2.131), and the results are

k[1] = 1.00 k[2] = 0.80 k[3] = 0.80

Using Eq. (2.132a), the values of the remaining ks for computing the upper bound are obtained as

k[4]u = max
1.00
k[5],U = max

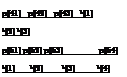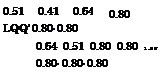and, by the same token, for the lower bound are

k[4], l = 0.51 X[5], l = 0.6375

Applying Eq. (2.120), along with Хц = (1.0, 0.8, 0.8, 0.8, 1.0), one obtains the upper bound for the multivariate normal probability Фц(z |Rx) = 0.01699. Similarly, using Xl = (1.0, 0.8, 0.8, 0.51, 0.6375), the lower bound is obtained as ФL(z |Rx) = 0.01697.

To use Eqs. (2.133a) and (2.133b) for computing the upper and lower bounds for the multivariate normal probability, the marginal probabilities and each pair of bivariate normal probabilities are computed first, according to Eq. (2.3). The results are

Ф(г1) = 0.1587 Ф( z2) = 0.02275 Ф(г3) = 0.5000 Ф( z4) = 0.9772 Ф(г5) = 0.8413

Ф(-z1, —z2) = 0.8395 Ф(-z1, —z3) = 0.4816

Ф(—z1, —z4) = 0.0226 Ф(—z1, —z5) = 0.1523

Ф(—z2, — z3) = 0.5000 Ф(—z2, —z4) = 0.0228 Ф(—z2, —z5) = 0.1585

Ф(—z3, —z4) = 0.0227 Ф(—z3, —z5) = 0.1403 Ф(—z4, —z5) = 0.0209

The lower and upper bounds of the multivariate probability can be obtained as 0.02070 and 0.02086, respectively.