Definitions of Reliability and Risk

In view of the lack of generally accepted rigorous definitions for risk and reliability, it will be helpful to define these two terms in a manner amenable to mathematical formulation for their quantitative evaluation for engineering systems. The unabridged Webster’s Third New World International Dictionary gives the following four definitions of risk:

1. “the possibility of loss, injury, disadvantage, or destruction,…;

2. someone or something that creates or suggests a hazard or adverse chance: a dangerous element or factor;

3. a: (i) the chance of loss or the perils to the subject matter of insurance

covered by a contract, (ii) the degree of probability of such loss; b: amount at risk;

c: a person or thing judged as a (specified) hazard to an insurer; d: … (insure…);

4. the product of the amount that may be lost and the probability of losing it [United Nations definitition]”

The unabridged Random House Dictionary lists the following definitions of risk:

1. “exposure to the chance of injury or loss;

2. insurance: a) the hazard or chance of loss; b) the degree of probability of such loss; c) the amount that the insurance company may lose; d) a person or

thing with reference to the hazard involved in insuring him, her, or it; e) the type of loss, such as life, fire, marine disaster, or earthquake, against which an insurance policy is drawn,

3. at risk…;

4. take or run a risk__ ”

The Oxford English Dictionary defines risk as

1. “a) hazard, danger; exposure to mischance or peril; b) to run a or the risk; c) a venturous course; d) at risk or high risk: in danger, subject to hazard; e) a person who is considered a liability or danger; one who is exposed to hazard;

2. the chance or hazard of commercial loss_____ Also,… the chance that is

accepted in economic enterprise and considered the source of (an entrepreneur’s) profit.”

With reference to the first definition of the first two (American) dictionaries, risk is defined herein as the probability of failure to achieve the intended goal. Reliability is defined mathematically as the complement of the risk. In some disciplines, often the nonengineering ones, the word risk refers not just to the probability of failure but also to the consequence of that failure, such as the cost associated with the failure (United Nations definition). Nevertheless, to avoid possible confusion, the mathematical analysis of risk and reliability is termed herein reliability analysis.

Failure of an engineering system can be defined as a situation in which the load L (external forces or demands) on the system exceeds the resistance R (strength, capacity, or supply) of the system. The reliability ps of an engineering system is defined as the probability of nonfailure in which the resistance of the system exceeds the load; that is,

ps = P (L < R) (1.1)

in which P ( ) denotes probability. Conversely, the risk is the probability of failure when the load exceeds the resistance. Thus the failure probability (risk) pf can be expressed mathematically as

pf = P (L > R) = 1 — ps (1.2)

Failure of infrastructures can be classified broadly into two types (Yen and Ang, 1971; Yen etal., 1986): structural failure and functional (performance) fail­ure. Structural failure involves damage or change of the structure or facility, therefore hindering its ability to function as desired. On the other hand, per­formance failure does not necessarily involve structural damage. However, the performance limit of the structure is exceeded, and undesirable consequences occur. Generally, the two types of failure are related. Some structures, such as dams, levees, and pavement to support loads, are designed on the concept of structural failure, whereas others, such as sewers, water supply systems, and traffic networks, are designed on the basis of performance failure.

In conventional infrastructural engineering reliability analysis, the only uncertainty considered is that owing to the inherent randomness of geophysi­cal events, such floods, rainstorms, earthquakes, etc. For instance, in hydrosys­tem engineering designs, uncertainties associated with the resistance of the hydraulic flow-carrying capacity are largely ignored. Under such circum­stances, the preceding mathematical definitions of reliability and failure prob­ability then are reduced to

ps = P(L < r*) and pf = P (L > r*) (1.3)

in which the resistance R = r * is the designated value of resistance, a deterministic quantity. By considering inherent randomness of annual maxi­mum floods, the annual failure probability pf for a hydraulic structure designed with a capacity to accommodate a T-year flood, i. e., r* = lT, is 1/T.

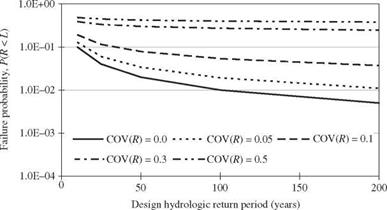
Figure 1.6 shows the effect of hydraulic uncertainty on the overall failure probability under the assumption that both random load and resistance are independent log-normal random variables. The figure can be produced eas­ily from the basic properties of log-normal random variables (see Sec. 2.6.2). Figure 1.6 clearly shows that by considering only inherent randomness of hydrologic load [the bottom curve corresponding to the coefficient of variation (COV), COV(R) = 0], the annual failure probability is significantly underesti­mated as the uncertainty of resistance COV(R) increases. As shown in Fig. 1.1, the inherent natural randomness of hydrologic processes is only one of the many uncertainties in hydrosystems engineering design. This figure clearly demonstrates the deficiency of the conventional frequency-analysis approach in reliability assessment of hydrosystems.

Figure 1.6 Effect of resistance uncertainty on failure probability under COV(L) = 0.1.