This approach starts with a selection of key components and modes of operation whose states (operational or failure) would decompose the entire system into simple series and/or parallel subsystems for which the reliability or failure probability can be evaluated easily. Then the reliability of the entire system is obtained by combining those of the subsystems using the conditional probability rule as
ps, sys — ps | Fm x ps, m + ps | Fm x pf, m (T.65)
in which ps | and ps | Fm are the conditional system reliabilities given that the
mth component is operational Fm and failed Fm, respectively, and ps, m and pf, m are the reliability and failure probabilities of the mth component, respectively.
Except for very simple and small systems, a nested conditional probability operation is inevitable. Efficient evaluation of system reliability of a complex system hinges entirely on a proper selection of key components, which generally is a difficult task when the scale of the system is large. Furthermore, the method cannot be adapted easily to computerization for problem solving.
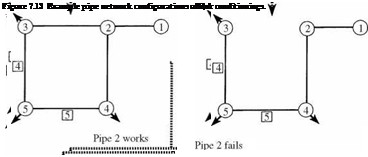
Example 7.15 Find the system reliability of the water distribution network in Fig. 7.9 using the conditional probability approach.
Solution Using the conditional probability approach for system reliability evaluation, first select pipe section 1 as the key element that decomposes the system into a simpler
configuration, as shown in Fig. 7.13. After the entire system is decomposed into a simple system configuration, the conditional probability of the decomposed systems can be evaluated easily. For example, the conditional system reliability, after imposing F1 and F3 for pipes 1 and 3, respectively, can be expressed as
Ps, sys | F[,F3 = P(F2 n F4n F5) = (0.95)3 = 0.8574
where ps | f ‘,f3 is conditional system reliability. Conditional system reliabilities for other imposed conditions are shown in Fig. 7.13. After the conditional system reliabilities for the decomposed systems are calculated, the reliability of the entire
 |
Original system
system can be combined using Eq. (7.65). For this particular example, the system reliability is
Ps, sys = Ps | F, F3 x P(F1, F3) + Ps | F, F3,F2 x P(F1, F3, F2)
+ Ps | F1,F,,F2 x P (F1> F3, F2)
= (0.8574)(0.95)(0.05) + (0.9975)(0.95)3 + (0.9025)(0.95)2(0.05)
= 0.9367
