The basic idea of reliability engineering is to determine the failure probability of an engineering system, from which the safety of the system can be assessed or a rational decision can be made on the design, operation, or forecasting of the system, as depicted in Fig. 1.3. For example, Fig. 1.4 schematically illustrates using reliability analysis for risk-based least-cost design of engineering infrastructures.
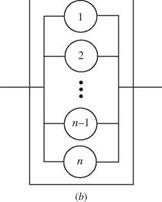
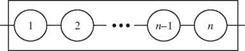
An infrastructure is a functioning system formed from a combination of a number of components. From the perspective of reliability analysis, infrastructure systems can be classified in several ways. First, they can be grouped according to the sequential layout of the components (Fig. 1.5). A series system is a system of components connected in sequence along a single path, i. e., in series. Failure of any one of the components leads to failure of the entire system. A parallel system is one with its components connected side by side,
i. e., in parallel paths. Many engineering systems have built-in redundancy such that they function as a parallel system. Failure occurs when none of the parallel alternative paths function. Second, from the view point of the time consistency of the statistical characteristics of the systems, they can be classified as a time — invariant statistically stationary system (or static system) and a time-varying statistically nonstationary system (or dynamic system).
Infrastructures may follow different paths to failure. The ideal and simplest type is the case that the resistance and loading of the system are statistically independent of time, or a stationary system. Most of the existing reliability analysis methods have been developed for such a case.
A more complicated but realistic case is that for which the statistical characteristics of the loading or resistance or both are changing with time, e. g., floods from a watershed under urbanization, rainfall under the effect of global
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
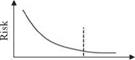
Figure 1.4 Risk-based least-cost design of infrastructural systems. (After Yen and Tung, 1993.)
warming, sewer or water supply pipes with deposition, and fatigue or elastic behavior of steel structure members. This case can further be subdivided into the subcases of (1) the changing process is irreversible and accumulative and (2) the changing process is reversible, e. g., repairable. For some infrastructures, the statistical characteristics of the system change with space or in time (or both), e. g., a reach of highway or levee along different terrains. There are other subsets ofthese time-varying or space-varying dynamic failure cases. One is the subcase that a component of the system already has malfunctioned, but failure has not occurred because the loading has not yet reached the level of such failure, or there is a redundant component to take the load, but the strength of the system is weakened. Another subcase is changing the tolerance of failure, such as changing acceptable standards by regulations.
|
|
|
