Computation of multivariate normal probability

Evaluation of the probability of multivariate normal random variables involves multidimensional integration as

Accurate evaluation for Ф(г |Rx) is generally difficult and often is resolved by approximations.

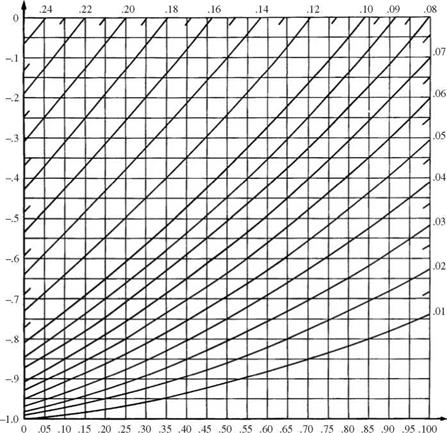
Bivariate normal probability. For abivariate case, Fortran computer programs for computing the lower left volume under the density surface, that is, Ф(а, b | p) = P(Z1 < a, Z2 < b | p), have been developed by Donnelly (1973) and Baughman (1988). The double integral for evaluating the bivariate normal probability can be reduced to a single integral as shown in Eq. (2.111). Sev­eral approximations have been derived (Johnson and Kotz, 1976). Derivation of bounds for the bivariate normal probability is presented in Sec. 2.7.3. For a bivariate normal probability, exact solutions have been obtained in the form of figures such as Fig. 2.28 for computing the upper-right volume under the bivari­ate standard normal density surface, that is, L(a, b | p) = P (Z1 > a, Z2 > b | p), in which L(a, b | p) can be expressed in terms of L(a, 0 | p) as

0, if (ab > 0 or ab = 0) and a + b > 0

1, otherwise 2

P L(a, 0lp) for 0 < a < 1 and -1 < p < 0. Values for a < 0 can be obtained using L(a, 01—p) = 0.5 — L(-a, 0lp) Figure 2.28 Bivariate normal cumulative distribution function. (After Abramowitz and Stegun, 1972.)

The relationship between Ф^, b | p) and L(a, b | p) is

Ф(a, b | p) = —1 + Ф^) + Ф(Ь) + L(a, b | p) (2.118)

From the definitions of Ф^, b | p) and L(a, b | p) and the symmetry of the bivari­ate normal PDF, the following relations are in order:

Ф^, to| p) = Ф^) Ф(то, b | p) = Ф(Ь) (2.119a)

L(a, — to | p) = 1 — Ф^) L(-to, b | p) = 1 — Ф(Ь) (2.119b)

P L(a, 0lp) for 0 < a < 1 and 0 < p < 1. Values for a < 0 can be obtained using L(a, 01—p) = 0.5 — L(-a, 0lp) Figure 2.28 (Continued)

L(a, b | p) = L(b, a | p) (2.119c)

L(-a, b | p) + L(a, b | —p) = 1 — Ф(Ь) (2.119d)

L(-h, —k | p) — L(k, h | p) = 1 — Ф(К) — Ф(к) (2.119e)

Example 2.21 Consider two correlated normal random variables X1 and X2 with

their statistical properties being

E(X1) = 10 Var(X1) = 9 E(X2) = 5 Var(X2) = 4 Cov(Xb X2) = 3.6

Compute P(X1 < 13, X2 < 3).

p

h

Figure 2.28 (Continued)

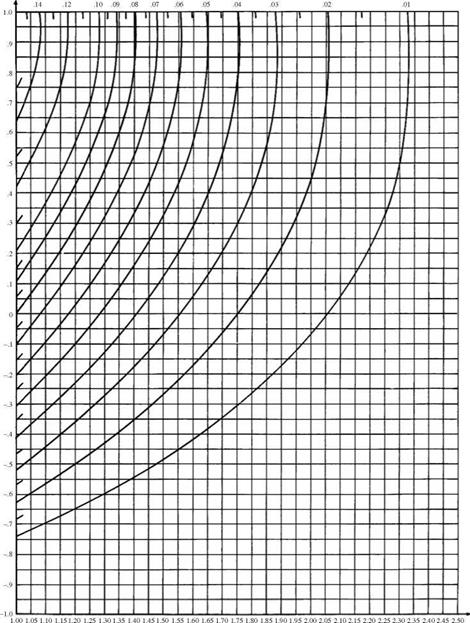
L(a, 0ip) for a > 1 and -1 < p < 1.

Values for a < 0 can be obtained using L(a, 01-p) = 0.5 — L(-a, 0lp)

Solution Based on the given information, the correlation coefficient between X1 and X2 is

Cov( X ь X2) 3.6 n„

P1,2 = ————————- = r — r — = 0.6

&X2 V9v4

Then

P(X! < 13, X2 < 3) = PIZ! < 13 — 10, Z2 < 3-5

= P(Zi < 1, Z2 < -11 P1,2 = 0.6) = ф(а = 1, b = -11 P12 = 0.6)

By Eq. (2.118),

Ф(1,-1|0.6) = -1 + Ф(1) + Ф(-1) + Д1, —1|0.6) Since ab = -1 < 0, according to Eq. (2.117),

,|й6)=К Чж)+К-Чж)- 2

= Д1, 0 | 0.894) + Д-1, 0 | 0.894) — 0.5

From Fig. 2.28b, Д1, 0 | 0.894) = 0.159. Since Д-1, 0 | 0.894) = 0.5 — L(1, 0 | -0.894), and according to Fig. 2.28a, by extrapolation, Д1, 0 | —0.894) = 0.004,

Д-1,0 | 0.894) = 0.5 — 0.004 = 0.496

Consequently, Д1, -11 0.6) = 0.159 + 0.496 — 0.5 = 0.155.

According to (a), the bivariate normal probability is Ф(1, -11 0.6) = Д1, -11 0.6) = 0.155. Alternatively, the bivariate normal probability can be computed by Eq. (2.121), and the result of the numerical integration for this example is 0.1569.

Multivariate normal probability. Johnson and Kotz (1976) show that if the correla­tion coefficient pij can be expressed as pij = XiXj for all i and j and |Xj | < 1, then each correlated standard normal random variable Zk can be represented by

Zk = Xk Z0 + J1 — Zk for k = 1> 2> ••• > K

where Z0, Z1, Z2,…, Z’Kare independent standard normal variables. The in­equality Zk < zk can be expressed as

iyl zk — Xkz0

Zk < —/

Then the multivariate normal probability can be calculated as

As can be seen from Eq. (2.120), the computation of the multivariate normal probability is reduced from multiple integrals to a single integral for which the result can be obtained accurately by various numerical integration techniques. (see Appendix 4A) Under the special case of equicorrelation, that is, ptj = p, for all i and j, the multivariate normal probability can be computed as

This equation, in particular, can be applied to evaluate the bivariate normal probability.

Under the general unequal correlation case, evaluation of multivariate nor­mal probability by Eq. (2.120) requires solving for K A’s based on K(K — 1)/2 different values of p in the correlation matrix Rx. This may not necessarily be a trivial task. Ditlevsen (1984) proposed an accurate algorithm by expanding Ф(г | Rx) in a Taylor series about an equal correlation pij = p > 0, for i = j. The equicorrelation p is determined in such a way that the first-order expansion term dФ(z | p) vanishes. The term dФ(z | p) can be expressed as

(2.122)

and Apij = pij — p. In computing the value of d Ф^ | p), numerical integration generally is required. However, one should be careful about the possible nu­merical overflow associated with the computation of ak (u) as the value of u gets large. It can be shown that by the L’Hospital rule, limu^TO ak(u) = 0 and

limu^-TO ak (u) = u.

Determination of the equicorrelation p for the expansion point can be made through the iterative procedure, as outlined in Fig. 2.29. A sensible starting value for p is the average of pij:

— 2

p = K (K — 1) ^ pij

KJ

Once such p is found, Ditlevsen (1984) suggests that the value of Ф(г | Rx) can be estimated accurately by a second-order approximation as

Ф(г |Rx) ^ Ф(г | p) + 1 d2Ф(г | p) (2.125)

in which Ф(г | p) is computed by Eq. (2.121), and the second-order error term is computed as

KKKK

(u)aj (u)a, r (u)as(u)(—br )Sir (—bs)SjsApij Aprs

i = 1 j = 1 r = 1 s = 1

(2.126)

where Sir is the Kronecker’s delta, having a value of 1 if i = r and otherwise 0, and

As can be seen, the evaluation of Ф(z |Rx) is reduced from a multiple integral to a single integral, which can be executed efficiently and accurately by many numerical integration algorithms.

For the univariate normal distribution, an asymptotic expansion of Ф(гО is (Abramowitz and Stegun, 1972) for z

(2.128)

This expansion for Ф(z) is smaller than every summand with an odd number of terms and is larger than every summand with an even number of terms. The truncation error decreases as the number of terms increases. Note that Eq. (2.128) is particularly appropriate for evaluating the normal tail probabil­ity. The expansion has been generalized by Ruben (1964) for the multivariate normal distribution as

in which the coefficients ak are elements in a vector a obtained from

a= Rx 1z

It should be noted that Eq. (2.130) is valid only when all coefficients ak are positive. The right-hand-side of Eq. (2.129) provides an upper bound for the multivariate normal probability.