Basic probability rules for system reliability

The solution approaches to system reliability problems can be classified broadly into failure-modes approach and survival-modes approach (Bennett and Ang, 1983). The failure-modes approach is based on identification of all possible fail­ure modes for the system, whereas the survival-modes approach is based on the all possible modes of operation under which the system will be operational. The two approaches are complementary. Depending on the operational char­acteristics and configuration of the system, a proper choice of one of the two approaches often can lead to significant reduction in efforts needed for the re­liability computation.

Consider that a system has M components or modes of operation. Let event Fm indicate that the mth component or mode of operation is in the failure state. If the system is a series system, the failure probability of the system is the probability that at least one of the M components or modes of operation fails, namely,

in which pf, sys is the failure probability of the system. On the other hand, the system reliability ps, sys is the probability that all its components or modes of operation perform satisfactorily, that is,

ps, sys = P(F1 n F2 n-.-n FM) = p( n F^ (7.2)

m=1 J

in which Fm is the complementary event of Fm indicating that the mth compo­nent or mode of operation does not fail.

In general, failure events associated with system components or modes of op­eration are not mutually exclusive. Therefore, referring to Eq. (2.4), the failure

probability for a series system can be computed as

n M M_1 M

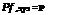mUi Fm) = £ P(Fm) _^ X) P(Fi, F,)

‘ m=1 i = l j =i + 1

+ EEE P (Fi, Fj, FA ) -… + (-1) MP (Fi, F2,…, Fm ) (7.3)

i< j < Л

According to Eq. (2.7), the reliability for a series system is

Ps, sys = P (F1) X P (F2 | F1) X P (FjJ | F1, F-2) X ••• x P (FM | F1, F-2,…, FM_1)

(7.4)

In the case that failure events Fm’s are mutually exclusive or the probability of joint occurrence of multiple failures is negligible, the failure probability of a series system can be easily obtained as

M

Pf, SyS = £ P(Fm) (7.5a)

m=1

with the corresponding system reliability

M

ps, sys = 1 _ pf, sys = 1 ^ ] P (Fm) (7.5b)

m=1

Under the condition that all failure events are statistically independent, the reliability of a series system can be computed easily as

MM

Ps, SyS = П P(Fm) HI [1 _ P(Fm)] (7.6a)

m=1 m=1

with the corresponding system failure probability

M

Pf, SyS = 1 _П [1 _ P(Fm)] (7.6b)

m=1

The component probability P(Fm) can be determined by methods described in Chaps. 4, 5, and 6 of this book.

Example 7.1 Consider a series system consisting of M independent components, each with an identical component reliability of ps. The system reliability, according to Eq. (7.6a), is

n — PM

Ps, sys = P s

Figure 7.4 shows the relationship among the reliability of a series system, component reliability, and the number of components. As can be seen, the reliability of a series system decreases as the number of components increases.

Figure 7.4 Relationship among reliability of a series system, component reliability, and the number of components.

In the case of a parallel system, the system would fail if all its components or modes of operation failed. Hence the failure probability for a parallel system is

Pf, sys = P(F1 n F2 П—П Fm) = P П Fm (7.7)

m=1

The reliability of a parallel system, on the other hand, is the probability that at least one of its component or modes of operation is functioning, that is,

Ps, sys = P (F1 U F2U-.-U FM) = P U Fm (7.8)

m=1

Hence, under the condition of independence for all failure events, the failure probability of a parallel system simply is

M

pf, sys = П P (Fm)

m=1

with the corresponding system reliability being

M

Ps, sys = 1 — П P (Fm) = 1 — П [! — P (Fm)]

m=1

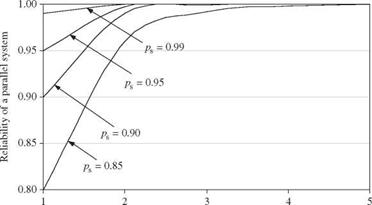
Example 7.2 Consider a parallel system consisting of M independent components, each with an identical component reliability of ps. The system reliability, according to Eq. (7.9b), is

Ps, sys = 1 — (1 — Ps )M

Figure 7.5 shows the relationship among reliability of a parallel system, component reliability, and the number of components. The figure indicates that the reliability of a parallel system increases as the number of components increases.

No. of components or operational modes Figure 7.5 Relationship among reliability of a parallel system, component reliability, and the number of components.

For mutually exclusive failure events, reliability of a parallel system can be computed as

M M

Pssys = P (Fm) = M — P(Fm) (7.10a)

m=1 m=l

with the corresponding system failure probability

M

Pf, sys = 1 + P (Fm) — M (7.10b)

m=l

Unfortunately, for a real-life system involving multiple components or modes of operation, the corresponding failure events are neither independent nor mu­tually exclusive. Consequently, the computation of exact values of system reli­ability and failure probability would not be a straightforward task. In practical engineering applications, bounds on system reliability are computed based on simpler expressions with less computational effort. As will be seen in the next subsection, to achieve tighter bounds on system reliability or failure probability, a more elaborate computation will be required. Of course, the required preci­sion for the computed system reliability is largely dependent on the importance of the satisfactory performance of the system under consideration.