Analysis*
Assessment of the reliability of a hydrosystems infrastructural system or its components involves the use of probability and statistics. This chapter reviews and summarizes some fundamental principles and theories essential to reliability analysis.
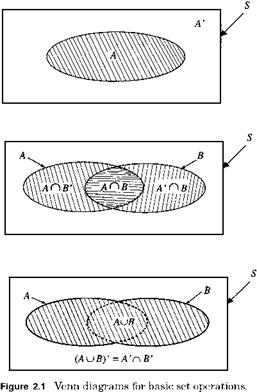
In probability theory, an experiment represents the process of making observations of random phenomena. The outcome of an observation from a random phenomenon cannot be predicted with absolute accuracy. The entirety of all possible outcomes of an experiment constitutes the sample space. An event is any subset of outcomes contained in the sample space, and hence an event could be an empty (or null) set, a subset of the sample space, or the sample space itself. Appropriate operators for events are union, intersection, and complement. The occurrence of events A and B is denoted as A U B (the union of A and B), whereas the joint occurrence of events A and B is denoted as A n B or simply (A, B) (the intersection of A and B). Throughout the book, the complement of event A is denoted as A. When two events A and B contain no common elements, then the two events are mutually exclusive or disjoint events, which is expressed as (A, B) = 0, where 0 denotes the null set. Venn diagrams illustrating the union and intersection of two events are shown in Fig. 2.1. When the occurrence of event A depends on that of event B, then they are conditional events,
*Most of this chapter, except Secs. 2.5 and 2.7, is adopted from Tung and Yen (2005).
Copyright © 2006 by The McGraw-Hill Companies, Inc. Click here for terms of use.
|
|
which is denoted by A | B. Some useful set operation rules are
1. Commutative rule: AU B = B U A; AП B = B П A.
2. Associative rule: (AU B) U C = AU (B U C); (AП B) n C = An (B n C).
3. Distributive rule: An (B U C) = (An B) U (An C); AU (B n C) = (AU B) n (A U C).
4. de Morgan’s rule: (AU BУ = An B’; (AnBУ = A’UB’.
Probability is a numeric measure of the likelihood of the occurrence of an event. Therefore, probability is a real-valued number that can be manipulated by ordinary algebraic operators, such as +, -, x, and /. The probability of the occurrence of an event A can be assessed in two ways. In the case where an experiment can be repeated, the probability of having event A occurring can be estimated as the ratio of the number of replications in which event A occurs nA versus the total number of replications n, that is, nA/n. This ratio is called the relative frequency of occurrence of event A in the sequence of n replications. In principle, as the number of replications gets larger, the value of the relative frequency becomes more stable, and the true probability of event A occurring could be obtained as
P (A) = lim„^TO—A (2.1)
n
The probabilities so obtained are called objective or posterior probabilities because they depend completely on observations of the occurrence of the event.
In some situations, the physical performance of an experiment is prohibited or impractical. The probability of the occurrence of an event can only be estimated subjectively on the basis of experience and judgment. Such probabilities are called subjective or prior probabilities.






Leave a reply