Vertical Alignment
The design of the vertical alignment of a roadway also has a direct effect on the safety and comfort of the driver. Steep grades can slow down large, heavy vehicles in the traffic stream in the uphill direction and can adversely affect stopping ability in the downhill direction. Grades that are flat or nearly flat over extended distances will slow down the rate at which the pavement surface drains. Vertical curves provide a smooth change between two tangent grades, but must be designed to provide adequate stopping sight distance.
Tangent Grades. The maximum percent grade for a given roadway is determined by its functional classification, surrounding terrain, and design speed. Table 2.16 shows how the maximum grade can vary under different circumstances. Note that relatively flat grade limits are recommended for higher functional class roadways and at higher design speeds, whereas steeper grade limits are permitted for local roads and at lower design speeds.
Concerning minimum grades, flat and level grades may be used on uncurbed roadways without objection, as long as the pavement is adequately crowned to drain the surface laterally. The preferred minimum grade for curbed pavements is 0.5 percent, but a grade of 0.3 percent may be used where there is a high-type pavement accurately crowned and supported on firm subgrade.
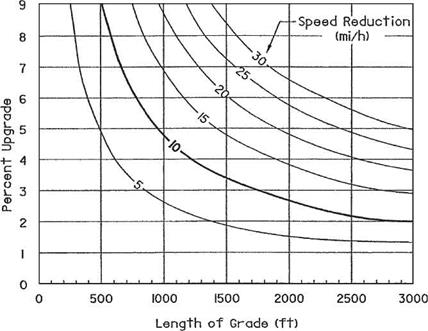
Critical Length of Grade. Freedom and safety of movement on two-lane highways are adversely affected by heavily loaded vehicles operating on upgrades of sufficient lengths to result in speeds that could impede following vehicles. The term critical length of grade is defined as the length of a particular upgrade which reduces the operating speed of a truck with a weight-to-horsepower ratio of 200 lb/hp (0.122 kg/W) to 10 mi/h (1.6 km/h) below the operating speed of the remaining traffic. Figure 2.11 provides the amount of speed reduction for these trucks given a range of percent upgrades and length of grades. The entering speed is assumed to be 70 mi/h (113 km/h). The curve representing a 10-mi/h (1.6-km/h) reduction is the design guideline to be used in determining the critical length of grade.
Design speed, mi/h
|
TABLE 2.16 Maximum Grades as Determined by Function, Terrain, and Speed, % Functional
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m. *Grades 1% steeper may be used for extreme cases where development in urban areas precludes the use of flatter grades. Grades 1% steeper may also be used for one-way down-grades except in hilly terrain. ^Grades 1% steeper may be used for short lengths (less than 500 ft) and on one-way down-grades. For rural highways with current ADT less than 400, grades may be 2% steeper. Source: Location and Design Manual, Vol. 1, Roadway Design. Ohio Department of Transportation, with permission. |
If after an investigation of the project grade line, it is found that the critical length of grade must be exceeded, an analysis of the effect of the long grades on the level of service of the roadway should be made. Where speeds resulting from trucks climbing up long grades are calculated to fall within the range of service level D or lower, consideration should be given to constructing added uphill lanes on critical lengths of grade. Refer to the “Highway Capacity Manual” (Ref. 10) for methodology in determining level of service. Where the length of added lanes needed to preserve the recommended level of service on sections with long grades exceeds 10 percent of the total distance between major termini, consideration should be given to the ultimate construction of a divided multilane facility.
|
FIGURE 2.11 Critical lengths of grade based on typical heavy truck of 200 lb/hp (0.122 kg/W) at entering speed of 70 mi/h (113 km/h). Notes: (1) This graph can also be used to compute the critical length of grade for grade combinations. For example, find the critical length of grade for a 4 percent upgrade preceded by 2000 ft (610 m) of 2 percent upgrade and a tolerable speed reduction of 15 mi/h (24 km/h). From the graph, 2000 ft (610 m) of 2 percent upgrade results in a speed reduction of 7 mi/h (11 km/h). Subtracting 7 mi/h (11.2 km/h) from the tolerable speed reduction of 15 mi/h (24 km/h) gives the remaining tolerable speed reduction of 8 mi/h (12.8 km/h). The graph shows that the remaining tolerable speed reduction would occur on 1000 ft (305 m) of the 4 percent upgrade. (2) The critical length of grade is the length of tangent grade. When a vertical curve is part of the critical length of grade, an approximate equivalent tangent grade should be used. Where A < 3 percent, the vertical tangent lengths can be used (VPI to VPI). Where A > 3 percent, about V4 of the vertical curve length should be used as part of the tangent grade. Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m. (From Location and Design Manual, Vol. 1, Roadway Design, Ohio Department of Transportation, with permission) |
Vertical Curves. A vertical curve is used to provide a smooth transition between vertical tangents of different grades. It is a parabolic curve and is usually centered on the intersection point of the vertical tangents. One of the principles of parabolic curves is that the rate of change of slope is a constant throughout the curve. For a vertical curve, this rate is equal to the length of the curve divided by the algebraic difference of the grades. This value is called the K value and represents the distance required for the vertical tangent to change by 1 percent. The K value is useful in design to determine the minimum length of vertical curve necessary to provide minimum stopping sight distance given two vertical grades.
Allowable Grade Breaks. There are situations where it is not necessary to provide a vertical curve at the intersection of two vertical grades because the difference in grades is not large enough to provide any discomfort to the driver. The difference
|
TABLE 2.17 Maximum Change in Vertical Alignment Not Requiring a Vertical Curve
Based on the following equation: . = 46.5L = 1162.5 A = V2 = V2 |
where A = maximum grade change, %
L = length of vertical curve, ft; assume 25 V = design speed, mi/h
Note: The recommended minimum distance between consecutive deflections is 100 ft (30 m) where design speed > 40 mi/h (64 km/h) and 50 ft (15 m) where design speed < 40 mi/h.
*Rounded to nearest 0.05%.
Source: Location and Design Manual, Vol. 1, Roadway
Design, Ohio Department of Transportation, with permission.
varies with the design speed of the roadway. At 25 mi/h (40 km/h), a grade break of 1.85 percent without a curve may be permitted, while at 55 mi/h (88 km/h) the allowable difference is only 0.40 percent. Table 2.17 lists the maximum grade break permitted without using a vertical curve for various design speeds. The equation used to develop the distances is indicated as well as a recommended minimum distance between consecutive grade breaks. Where consecutive grade breaks occur within 100 ft (30 m) for design speeds over 40 mi/h (64 km/h), or within 50 ft (15 m) for design speeds at 40 mi/h (64 km/h) and under, this indicates that a vertical curve may be a better solution than not providing one.
Crest Vertical Curves. The major design consideration for crest vertical curves is the provision of ample stopping sight distance for the design speed. Calculations of available stopping sight distance are based on the driver’s eye 3.5 ft (1.07 m) above the roadway surface with the ability to see an object 2 ft (0.61 m) high on the roadway ahead over the top of the pavement. Table 2.18 lists the calculated design stopping sight distance values and the corresponding K values for design speeds from 20 to 70 mi/h (32 to 113 km/h). The values shown are based on the assumption that the curve is longer than the sight distance. In those cases where the sight distance exceeds the vertical curve length, a different equation is used to calculate the stopping sight distance provided. The equations are shown in the table.
Another consideration in designing crest vertical curves is passing sight distance, especially when dealing with two-lane roadways. This has already been discussed
Height of eye, 3.50 ft; height of object, 2.00 ft
|
TABLE 2.18 Stopping Sight Distance (SSD) for Crest Vertical Curves at Design Speeds from 20 to 70 mi/h (32 to 113 km/h)
|
Using S = stopping sight distance, ft
L = length of crest vertical curve, ft A = algebraic difference in grades, %, absolute value K = rate of vertical curvature, ft per % change
• For a given design speed and A value, the calculated length L = KA.
• To determine S with a given L and A, use the following:
For S < L: S = 46.45VK where K = L/A
For S > L: S = 1079/A + L/2
Conversions: 1 mi/h = 1.609 km/h, 1 ft = 0.305 m.
Note: For design criteria pertaining to collectors and local roads wih ADT less than 400, please refer to the AASHTO publication, Guidelines for Geometric Design of Very Low-Volume Local Roads (ADT < 400).
Source: Location and Design Manual, Vol. 1, Roadway Design, Ohio
Department of Transportation, with permission.
under “Passing Sight Distance” earlier in this chapter. Also, in addition to being designed for safe stopping sight distance, crest vertical curves should be designed for comfortable operation and a pleasing appearance whenever possible. To accomplish this, the length of a crest curve in feet should be, as a minimum, 3 times the design speed in miles per hour.
Sag Vertical Curves. The main factor affecting the design of a sag vertical curve is headlight sight distance. When a vehicle traverses an unlighted sag vertical curve at night, the portion of highway lighted ahead is dependent on the position of the headlights and the direction of the light beam. For design purposes, the length of roadway lighted ahead is assumed to be the available stopping sight distance for the curve. In calculating the distances for a given set of grades and a length of curve, the height of the headlight is assumed to be 2 ft (0.61 m) and the upward divergence of the light beam is considered to be 1°. Table 2.19 lists the calculated design stopping sight distance values and the corresponding K values for design speeds from 20 to 70 mi/h (32 to 113 km/h). As was the case with crest curves, the values shown are based on the assumption that the curve is longer than the sight distance. In those cases where the sight distance exceeds the vertical curve length, a different equation is used to calculate the actual stopping sight distance provided as indicated in the table.
Note for sag curves, when the algebraic difference of grades is 1.75 percent or less, stopping sight distance is not restricted by the curve. In these cases, the equations in Table 2.19 will not provide meaningful answers. Minimum lengths of sag vertical curves are necessary to provide a pleasing general appearance of the highway. To accomplish this, the minimum length of a sag curve in feet should be equal to 3 times the design speed in miles per hour.
Vertical Alignment Considerations. The following items should be considered when establishing new vertical alignment:
• The profile should be smooth with gradual changes consistent with the type of facility and the character of the surrounding terrain.
• A “roller-coaster” or “hidden dip” profile should be avoided.
• Undulating grade lines involving substantial lengths of steeper grades should be appraised for their effect on traffic operation, since they may encourage excessive truck speeds.
• Broken-back grade lines (two vertical curves—a pair of either crest curves or sag curves—separated by a short tangent grade) should generally be avoided.
• Special attention should be given to drainage on curbed roadways where vertical curves have a K value of 167 or greater, since these areas are very flat.
• It is preferable to avoid long, sustained grades by breaking them into shorter intervals with steeper grades at the bottom.






Leave a reply