Plastic Pipe
Introduction. Gravity flow thermoplastic pipes used in highway drainage applications are typically manufactured of high-density polyethylene (HDPE) or polyvinyl chloride (PVC). To a lesser extent acrylonitrile-butadiene-styrene (ABS) pipe is also used but is limited to drain, waste, and vent applications. Plastic pipes are always circular in crosssection. They may be either of a solid wall or profile wall design. These structures are generally designed for ring thrust by a semiempirical method that includes checks for wall area, buckling, and wall stress and strain. A check is also made to ensure the structure has sufficient rigidity to withstand handling and installation forces. Thermoplastic pipes may also be designed using finite-element computer programs that model both the structure and the soil. One such program, CANDE (“Culvert Analysis and Design,” PC-TRANS, Kansas University Transportation Center, Lawrence), includes a solution based on the theoretical work of Burns and Richard (“Attenuation of Stresses for Buried Cylinders,” Proceedings of Symposium on Soil-Structure Interaction, University of Arizona, Tucson, 1964). The Burns and Richard solution is derived from generalized shell theory. The authors derived equations using a linear elastic shell in a linear elastic medium. While a thermoplastic pipe buried in soil is not a linear elastic shell in a linear elastic medium, the derived equations have been shown to have general suitability for deep burial conditions.
The current design specifications for thermoplastic pipes are rapidly evolving. There is significant research in the areas of profile design, material quality control, and long-term pipe response. One particularly interesting area is the area of profile design. Thermoplastic pipes, with the multitude of wall profiles, can be vulnerable to local wall buckling. While a localized wall buckle will rarely lead to pipe failure, it can reduce the effective physical properties of the pipe profile. AASHTO has adopted equations for determining the postbuckling physical properties of the pipe profile.
There has been no standardization of the wall profiles. Manufacturers have significant leeway in designing the pipe wall profile. General mechanical and physical properties of the more common thermoplastic materials are given in Tables 5.22 and 5.23. Because of this lack of standardization, the values in the tables do not necessarily represent any manufactured pipe products, but rather are the critical design values for
|
TABLE 5.22 Dimensional Data for Plastic Pipes
Conversions: 1 in = 25.4 mm, 1 in2/ft = 2.117 mm2/mm, 1 in4/in = 16,387 mm4/mm. *These sizes are covered in AASHTO Provisional Standard Specification for Corrugated Polyethylene Pipe, AASHTO Designation MP6-95. Source: Standard Specifications for Highway Bridges, AASHTO, with permission. |
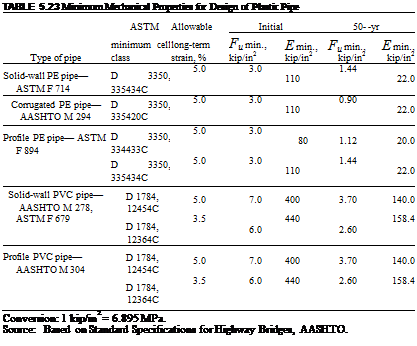 |
each property. It is highly unlikely that any one product could be produced to meet all of these minimum values. Material and physical properties for a specific pipe product should be obtained from the pipe manufacturer. The tables list both long-term and initial values for tensile strength and modulus of elasticity. Use short-term values for determining the response of the pipe to live loads. Use long-term values for determining the buckling capacity of the pipe. In determining the thrust response, use short-term values if the full soil prism is used for the dead load, and use long-term values if the dead load is factored through the use of the vertical arching factor.
Loads on Plastic Pipe. As discussed in Art. 5.8.2, live loads are distributed through the cover above the top of the pipe. In lieu of more exact computations, the live load pressures used for corrugated metal pipe, given in Table 5.19, can be used. The table also includes pressures for an H 25 wheel load, which is 25 percent greater than the H 20 wheel load, and an E 80 railway loading. All of the pressures in the table include an impact allowance for shallow cover.
Earth loads on flexible pipes can be highly variable. An investigation of the theoretical work of Burns and Richard by Dr. T. McGrath revealed that the pipe hoop stiffness is the critical factor in determining the pressure distribution about the pipe. The earth load on a thermoplastic pipe can be stated as a proportion of the soil prism load, similar to concrete and corrugated metal pipes. Based on the previously mentioned work of McGrath, the vertical arching factor (VAF) for thermoplastic pipes is
![]()
![]() Sh – 1.17 SH + 2.92
Sh – 1.17 SH + 2.92
![]()
, = AMR ‘H = EA
where SH = hoop stiffness factor
MS = constrained soil modulus, lb/in2 (see Table 5.24)
R = radius to centroid of pipe, in E = long-term, 50-year modulus of elasticity, lb/in2 A = cross-sectional area of corrugation, in2/ft
In determining the dead load on the pipe, the designer may use either the soil prism load or the load factored through the use of the vertical arching factor. If the factored load is used, AASHTO requires a check of the local stability of the profile wall section. The details of the local stability check can be found in the AASHTO publication
|
TABLE 5.24 Design Values for Constrained Soil Modulus, Ms
Conversions: 1 lb/ft2 = 0.0479 kPa, 1 lb/in2 = 6.895 X 10~3 MPa. Notes: (1) The soil types are defined by a two-letter designation that indicate general soil classification, Sn for sands and gravels, Si for silts, and Cl for clays. Specific soil groups that fall into these categories should be based on ASTM D 2487 and AASHTO M 145. (2) The numerical suffix to the soil type indicates the compaction level of the soil as a percentage of maximum dry density determined in accordance with AASHTO T-99. Source: From Design Method for Flexible Pipe, AASHTO, 1998, with permission. |
LRFD Bridge Design Specifications. If the full soil prism is used, the profile stability check can be conservatively ignored.
The total load (pressure) is then calculated as follows: The design is calculated by multiplying the dead load by a p factor of 1.5 and the live load by a factor of 1.67. The summation of the dead load and live load is then multiplied by a у factor of 1.3.
Structural Design of Plastic Pipe. Calculations proceed as follows. The thrust in the pipe wall is
![]()
![]() (5.49)
(5.49)
where TL = factored thrust, lb/ft
PL = factored load pressure, lb/ft2 S = pipe diameter or span, in
The required wall area to resist the thrust is
where A = required wall area, in2/ft
fu = minimum tensile strength, lb/in2 ф = capacity modification factor, 1.0
Next, check for possible wall buckling. The critical buckling pressure must be greater than the factored design load pressure. The critical buckling pressure (lb/in2 or kPa) is given by the following equation:
where Ms = constrained soil modulus, lb/in2 (see Table 5.24)
R = radius to centroid of pipe, in E = modulus of elasticity, lb/in2 I = moment of inertia of pipe profile, in4/in v = Poisson ratio, 0.4
Thermoplastic materials must also be checked to ensure that total wall strains do not exceed the resistance capabilities of the plastic. The pipe wall must resist the combined action of bending and thrust. Compressive strain is the critical strain since wall thrust acts purely in compression and will tend to decrease the tensile strain in the wall. Maximum permissible strain values are given in Table 5.23. The bending strain in the wall can be calculated as
where Df = pipe shape factor (see Table 5.25)
R = radius to centroid of pipe, in
ymax = distance from centroid of pipe wall to furthest pipe surface, in Д = vertical deflection, in ф = capacity modification factor, 0.5
|
TABLE 5.25 Shape Factors for Design of Plastic Pipe
Notes: (1) Interpolate for intermediate pipe stiffness values. (2) For Class IA and IB backfill materials, use the appropriate “Gravel” column. (3) For Class IVA backfill material, use the highest shape factor for that pipe stiffness. (4) Information has been modified from ANSI/AWWA C950-88, p. 28, for pipe stiffnesses appropriate for corrugated polyethylene pipe. (5) SPD = specified minimum density. Source: From Structural Design Method for Corrugated Polyethylene Pipe, Corrugated Polyethylene Pipe Association, 2000, with permission. |
and the compressive hoop, or circumferential, strain is
where all variables are as described above.
The total compressive wall strain, є, is determined by adding the bending strain and hoop strain:
є = Єь + Єh (5.54)
The equation for determining the bending strain includes the pipe vertical deflection as a design input parameter. Traditionally, the modified Iowa equation has been used to estimate expected pipe deflections. However, differences between calculated and field measured values as great as 100 percent have been reported. This is not a criticism of the equation. It certainly has applicability for small deflection pipe products such as concrete or corrugated metal. Further, with all of the technological advancements in computer modeling, to date no better equation or method has been developed.
In lieu of calculating the expected pipe deflection via the modified Iowa equation, the designer may set a maximum permissible in-field deflection limit in the project specifications. This deflection value can then be used in the design calculations without worry about the accuracy of the computed value.
Example: Thermoplastic Pipe Design. A 42-in-diameter (1050 mm) culvert is required for a site with 6 ft (1.83 m) of cover and an HS 20 live load. The pipe will be installed with a well-graded gravel backfill compacted to 95 percent of Proctor density. The maximum in-field deflection will be 5 percent. The pipe is an HDPE pipe with the following material properties:
Dt = inside pipe diameter, 41.85 in (1063 mm)
A = pipe wall area, 6.420 in2/ft (13.6 mm2/mm)
I = moment of inertia, 0.621 in4/in (10,176 mm4/mm)
c = distance to the centroid of the pipe wall, 1.38 in (35.0 mm)
E = modulus of elasticity, 110,000 lb/in2 (758 MPa)
fu = minimum tensile strength, 900 lb/in2 (6.21 MPa)
First, calculate the design load pressure as follows:
1.3 (1.5 X 771.6 + 1.67 X 200)
1938.8 lb/ft2 (92.8 kPa)
Then, from Eq. (5.49), the factored thrust in the pipe wall is
3392.9 lb/ft (49.5 kN/m)
From Eq. (5.50), the required wall area to resist the thrust is
A
3392.9
1.0(3000) 1.13 in2/ft (2.39 mm2/mm)
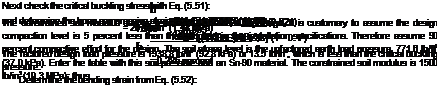 |
1938.8(41.85 + 1.38)
12(6.42)(110,000)
= 0.990 percent
The total compressive wall strain is 0.285 percent + 0.990 percent = 1.275 percent. This is less than the permissible 5 percent for HDPE, and therefore the design is acceptable.






Leave a reply