Jointed Rigid Pavement
Jointed rigid pavements tend to crack at 13 to 25 ft (4 to 8 m) lengths because of (1) initial shrinkage after placement as excess water evaporates, (2) temperature-induced expansion and contraction resisted by friction with the subgrade, (3) curling and warping caused by temperature and moisture differences between the top and bottom of the slab, and (4) load – induced stresses.
As slabs contract as a result of seasonal temperature changes, cracks form and widen, or formed joints widen, allowing incompressible materials into the cracks or joints. Subsequently, expansion is hindered and pressure is built up in the pavement. This pressure can result in pressure spalling or even blowups. To control this, partial depth saw cuts are made at regular intervals which induce concrete to crack at these locations. The timing and depth of these saw cuts are critical to ensure that the pavement cracks at the controlled location. Saw cuts should be made as soon as the pavement can support the weight of the saw and operator. The saw cuts should be made at a depth of one-third of the slab thickness for longitudinal joints, and one-fourth of the slab thickness for transverse joints. These saw cuts are then sealed with some type of joint sealer to prevent intrusion of incompressibles. If the saw cut interval (joint spacing) is short enough, intermediate cracks are eliminated. If longer intervals are used, intermediate cracks will form.
Load transfer is the critical element at joints and cracks. In undowelled, unreinforced pavements, any load transfer must be provided by aggregate interlock.
|
FIGURE 3.1 Typical contraction joint in rigid pavement with dowel for positive load transfer. Conversion: 1 in = 25.4 mm. |
|
FIGURE 3.2 Typical contraction joint in rigid pavement without dowel for load transfer. Conversion: 1 in = 25.4 mm. |
Aggregate interlock is lost when slabs contract and the joints or cracks open up. Also, interlock is slowly destroyed by the movement of the concrete as traffic passes over. Given large temperature variations and heavy trucks, aggregate interlock is ineffectual, and faulting is the primary result.
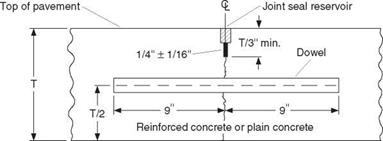
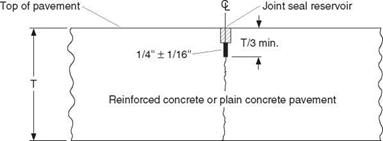
To provide load transfer at the joints, dowels are used which allow for expansion and contraction. Figure 3.1 illustrates a typical doweled joint with saw cut and joint seal. Figure 3.2 shows a similar joint without the dowel to provide load transfer.
Where a long joint spacing is used and intermediate cracks are expected, steel reinforcement is added to hold the cracks tightly closed (JRCP). This allows the load transfer to be accomplished through aggregate interlock without the associated problems described above. Contraction joints do not provide for expansion of the pavement unless the same amount of contraction has already taken place. This contraction will initially be from shrinkage due to concrete curing. Later changes in the pavement length are due to temperature changes.
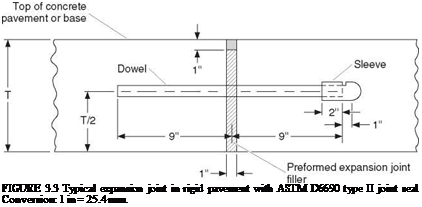
Where fixed objects such as structures are placed in the pavement, the use of an expansion joint is warranted. Expansion joints should be used sparingly. The pavement will be allowed to creep toward the expansion joint, thus opening the adjacent contraction joints. This can cause movement in the adjacent contraction joints in excess of their design capabilities and result in premature failures. Figure 3.3 shows a detail for a typical expansion joint.
The design of reinforcing steel is a function of seasonal temperature change, subbase friction, and the weight of the slab. Inadequate reinforcing will not be able to hold the
 |
cracks together, and faulting will result. The amount of reinforcing needed to hold cracks together is traditionally calculated using a relationship based on the friction between the subgrade and the bottom of the slab. This relationship assumes that for a crack to open enough to fail the aggregate interlock, the slab will have to slide along the subbase. The current AASHTO recommendation is based on this traditional approach (Guide for Design of Pavement Structures, American Association of State Highway and Transportation Officials, 1993).
The relationship can be expressed as follows:
where As = area of steel required, in2/ft of width (mm2/mm)
W = weight of slab, lb/ft2 (MPa)
F = coefficient of resistance between slab and subgrade (1.5 unless otherwise known)
L = length of slab, ft (mm)
fs = allowable stress in steel, lb/in2 (MPa)
Although these relationships are accepted by most leading authorities and are referred to in almost every reference on the subject, it is important to understand that they make many assumptions about physical quantities that are seldom consistent throughout a length of pavement. For instance, the friction factor can be affected by something as insignificant as a large footprint in the base course prior to paving. Additionally, the environment can play an important role as water and salt erode the steel, thus reducing the sectional area of the steel.
Where reinforcement is not desired, slab lengths must be chosen so that intermediate transverse cracks are eliminated. The most current theory used to determine allowable slab lengths involves a very old concept developed by Dr. H. M. Westergaard. Westergaard defined a constant called the radius of relative stiffness as an algorithm that relates the modulus of subgrade reaction to the flexural stiffness of the slab. Research indicates that cracking can be expected when the ratio between the slab length
and the radius of relative stiffness is greater than 5. The radius can be calculated from the following equation (Federal Highway Administration Technical Advisory T 5040.30, November 30, 1990):
where l = radius of relative stiffness, in (mm)
E = modulus of elasticity of concrete, lb/in2 (MPa) h = pavement thickness, in (mm)
k = modulus of subgrade reaction, (lb/in2)/in (MPa/mm) v = Poisson’s ratio (0.15)






Leave a reply