Critical Flow Depth
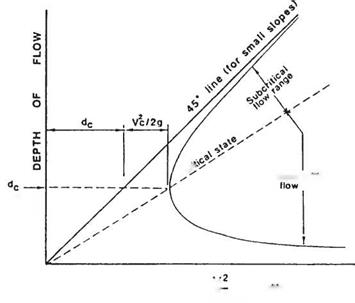
When the depth of flow is plotted against the specific energy, the specific energy diagram may be obtained and the critical depth found as illustrated in Fig. 5.5. The critical depth is defined as that depth where the specific energy is minimum. The flow velocity at the
 ШШїші
ШШїші
HTDKAUlic graoe LINE
channel bottom
DATUM LINE
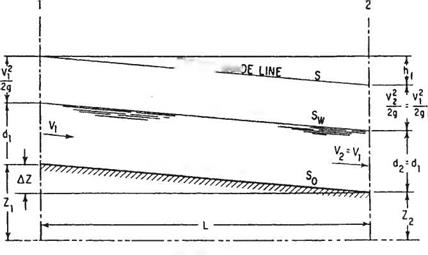
FIGURE 5.4 Flow characteristics for uniform open-channel flow. (From F. S. Merritt, ed., Standard Handbook for Civil Engineers, McGraw-Hill, 2004, with permission)
Supercritical
range
(critical
depth)
![]() (Specific energy)
(Specific energy)
FIGURE 5.5 Specific energy diagram. (From Highway Design Manual, California Department of Transportation, with permission)
critical depth is called the critical velocity. The channel slope that causes the critical depth and critical velocity is termed the critical slope. If the depth is greater than the critical depth, the flow is said to be subcritical and the velocity head reduces. Where the depth is less than the critical depth, the flow is said to be supercritical and the velocity head increases. For any particular energy level, except where the depth is critical, there are two corresponding depths that may occur. However, the depth may not alternate between these two values without a change in the channel configuration or slope.
Although the critical depth gives the greatest discharge, flow that causes the depth to be close to critical should be avoided, and thus the critical slope should be avoided. Flows near the critical depth may be turbulent. Inspection of the specific energy diagram reveals that where the depth is close to the critical depth, it takes little energy to change the flow from subcritical to supercritical or the reverse. If the flow does change from subcritical to supercritical, a hydraulic jump will occur. If placing the depth of flow near critical is unavoidable, it is advisable to assume the least favorable type of flow for design purposes. The critical depth may be determined from the following relationship:
![]() TT = 62 T g
TT = 62 T g
where A = cross-sectional flow area, ft2 (m2)
T = top width of channel flow, ft (m)
Q = discharge, ft3/s (m3/s) g = acceleration of gravity, 32.2 ft/s2 (9.8 m/s2)
For a channel with vertical walls, the velocity corresponding to the critical depth is given by
where Vc = critical velocity, ft/s (m/s). Also, for a channel with vertical walls, the flow area at a point of critical depth dc is
![]() A = T(dc)
A = T(dc)
Substitution in Eq. (5.14) leads to
It can be seen from this relationship that for a given flow, as the width of the channel changes the critical depth also changes. Such locations should be investigated for a hydraulic jump.
Points of control are locations where the depth of flow may be easily determined. The critical depth is one point of control and may be found in several typical locations. As discussed above, one of these locations may be where there is a change in the channel section. Other typical locations are where the slope changes abruptly from flat (subcritical) to steep (supercritical), at the crest of an overflow dam or weir, and at the outlet of a culvert on a subcritical slope discharging into a basin or wide channel.
The Froude number (Fr) may also be used in determining whether the channel is under supercritical, critical, or subcritical flow:
![]() V
V
(gdh)1/2
where d. = A/T. If Fr < 1.0, the channel flow is subcritical; if Fr = 1.0, the channel flow is critical; and if Fr > 1.0, the channel flow is supercritical.
Water surface profiles for the gradually varying flow condition may be determined by either the direct step method or the standard step method. The former method is applicable only to straight prismatic channel sections with gradually varying areas of flow. The standard step method may be used in nonprismatic channel sections and channel alignments that are not straight. Where the flow is subcritical, the analysis for determination of the water profile begins at the control point and proceeds upstream. Where the flow is supercritical, the opposite is true. (See V. T. Chow, Open-Channel Hydraulics, McGraw-Hill, 1959; and F. S. Merritt, ed., Standard Handbook for Civil Engineers, McGraw-Hill, 1996.)
Example: Critical Depth and Critical Velocity. A channel has a width of 10 ft (3 m)
and vertical sides. Determine the critical flow depth and critical velocity for a flow of 1000 ft3/s (28 m3/s).
U. S. Customary units:
From Eq. (5.17), dc = (Q2/gT 2)1/3 = [(1000)2/32.2(10)2]1/3 = 6.77 ft.
From Eq. (5.16), A = T(dc) = 10(6.77) = 67.7 ft2.
From Eq. (5.15), the critical velocity is Vc = (gA/T )1/2 = (32.2 X 67.7/10)1/2 = 14.8 ft/s. SI units:
From Eq. (5.17), dc = [(28)2/9.8(3)2]1/3 = 2.07 m.
From Eq. (5.16), A° = 3(2.07) = 6.21 m2.
From Eq. (5.15), Vc = (9.8 X 6.21/3)1/2 = 4.5 m/s.






Leave a reply