Corrugated Metal Pipe
Introduction. Corrugated metal structures are typically manufactured of either steel or aluminum. These structures are generally designed for ring thrust by a semiempirical method that includes checks for wall area, buckling, and seam strength. A check is also
|
FIGURE 5.39 Coefficients for calculating moment (M), thrust (N), and shear (V) in concrete pipe under linear pressure distributions. The coefficients used are as follows: M = CmWR, N = CnW, V = CW, where W is total load in each case and R is mean radius. Sign convention: +M is tension on inside face, +N is compression, +V is positive shear for left side. (From J. M. Paris, "Stress Coefficients for Large Horizontal Pipes," Engineering News Record, vol. 87, no. 19, November 10, 1921, with permission) |
made to ensure the structure has sufficient rigidity to withstand handling and installation forces. Computer programs for the design of corrugated steel pipe are available from the National Corrugated Steel Pipe Association, located in Dallas, Texas. Corrugated metal structures may also be designed using finite-element computer programs that model both the structure and the soil. The design procedure for metal box culverts and long-span structures differ somewhat from those of other corrugated metal structures.
Various methods are available for the design of corrugated metal pipe, arches, and pipe arches. Service load design is implemented by the use of safety factors that are applied to the yield stress, buckling stress, or seam strength to determine an allowable stress. Load factor design is utilized by applying load factors (P and 7) to the dead and
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Source: From Handbook of Steel Drainage and Highway Construction Products, American Iron and Steel Institute, 1994, with permission.
live loads and allowing the design stresses to approach the yield stress of the material adjusted by a capacity reduction factor (ф). Load and Resistance Factor Design (LRFD) is similar but differs in details.
The calculations include checks for wall area, buckling, and installation strength. In addition, the seam strength must be checked for annular corrugated and structural – plate pipe, arches, and pipe arches.
Values for moments of inertia and wall area of steel products are given in Table 5.18, and minimum longitudinal seam strengths for steel structural plate are given in Table 5.19. Data for aluminum products can be found in the AASHTO specifications.
Loads on Corrugated Metal Pipe. As discussed in Art. 5.8.2, live loads are distributed through the cover above the top of the pipe. In lieu of more exact computations, the live load pressures given in Table 5.20 are often used. The table also includes pressures for an H 25 wheel load, which is 25 percent greater than the H 20 wheel load, and an E 80 railway loading. All of the pressures in the table include an impact allowance for shallow cover.
TABLE 5.19 Minimum Longitudinal Seam Strength for 6- X 2-in Steel Structural Plate
Minimum seam strength,
kip/ft (kN/m) for indicated bolt pattern
|
2 bolts per 3 bolts per 4 bolts per Specified thickness, in (mm) corrugation corrugation corrugation
Source: Based on Standard Specifications for Highway Bridges, AASHTO. |
|
TABLE 5.20 Highway and Railway Live Loads
*See ASTM A796. Neglect live load when less than 100 lb/ft2 (4.8 kPa); use dead load only. Source: From Handbook of Steel Drainage and Highway Construction Products, American Iron and Steel Institute, 1994, with permission. |
The earth load is considered to be the full soil prism load. This is because the vertical arching factor for corrugated metal pipe is nearly unity.
AASHTO calculations for load (pressure) are as follows. The design load pressure, P, for service load design is the sum of the applicable live load plus impact and earth load. For load factor design, the design load is calculated by multiplying the dead load by a P factor of 1.5 and the live load by a factor of 1.67. The summation of the dead load and live load is then multiplied by a 7 factor of 1.3.
Structural Design of Pipe by Service Load Design. Calculations for factory-corrugated or structural-plate structures proceed as follows: The thrust in the pipe wall is
T = P ^|) (5.37)
where T = wall thrust, lb/ft (kN/m)
P = design load pressure, lb/ft2 (kPa)
S = pipe diameter or span, ft (m)
The required wall area to resist the thrust is
A = | (5.38)
a
where A = required wall area, in2/ft (mm2/mm)
fa = allowable stress, lb/in2 (MPa) = f/SF = minimum yield stress (lb/in2) (MPa) divided by safety factor (2.0)
For steel, fy = 33,000 lb/in2 (230 MPa); for aluminum, fy = 24,000 lb/in2 (170 MPa).
After selecting a corrugation profile and sheet thickness, check for possible wall buckling. If the buckling stressfcr is less than the minimum yield stress, recalculate the required wall area using fcr for the yield stress in lieu offy. The buckling stress is given by the following equations:
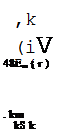 |
||||
If
where fcr = critical buckling stress, lb/in2 (MPa) fu = 45,000 lb/in2 (steel pipe) (310 MPa)
= 31,000 lb/in2 (aluminum pipe) (210 MPa)
= 35,000 lb/in2 (240 MPa) (aluminum structural plate 0.100-0.175 in or 2.54-4.44 mm thick)
= 34,000 lb/in2 (235 MPa) (aluminum structural plate 0.176-0.250 in or 4.47-63.5 mm thick) k = soil stiffness factor = 0.22 S = pipe diameter or span, in (mm) r = radius of gyration of corrugation = V//A, in (mm)
Em = modulus of elasticity of metal, lb/in2 (MPa)
= 29,000,000 lb/in2 (20 00 X 103 MPa) (steel) or 10,000,000 lb/in2 (69 X 103 MPa) (aluminum)
I = moment of inertia of corrugation, in4/in (mm4/mm)
A = cross-sectional area of corrugation, in2/in (mm2/mm)
Pipe with annular corrugations is fabricated with longitudinal seams, and a seam strength check is required. Helically corrugated pipe has no longitudinal seams, and therefore such a check is not required. For pipe fabricated with longitudinal seams, the required seam strength is
SS = T (SF) (5.41)
where SS = required seam strength, lb/ft (kN/m)
T = wall thrust, lb/ft (kN/m)
SF = safety factor = 3.0
Check handling and installation rigidity by calculating the flexibility factor FF, in/lb:
S 2
FF = f – (5.42)
EmI
where terms are as defined above. Limit FF to the values listed in Table 5.21.
Example: Corrugated Steel Pipe Design via Service Load Design. A 48-in-diameter (1200-mm) culvert is required for a site with 6 ft (1.83 m) of cover and an HS 20 live load. Determine a suitable corrugation and sheet thickness. Use factory-corrugated pipe with a helical lock seam.
|
TABLE 5.21 Maximum Flexibility Factors for Metal Culverts
Conversions: 1 in = 25.4 mm, 1 in/lb = 5.70 mm/N. Source: Based on Standard Specifications for Highway Bridges, AASHTO. |
![]()
First calculate the design load as follows: From Table 5.20, the live load pressure for the 6 ft (1.83 m) of cover is 200 lb/ft2 (9.6 kPa). The earth load pressure is the pressure from the soil prism load, Eq. (5.26):
The design load pressure is the sum of these loads:
P = 771.6 + 200 = 971.6 lb/ft2 (46.5 kPa) Then, from Eq. (5.37), the thrust in the pipe wall is
= 1943 lb/ft (28.4 kN/m)
From Eq. (5.38), the required wall area to resist the thrust is
![]() ff
ff
fa
1943
= 33,000/2
= 0.118 in2/ft (0.250 mm2/mm)
From Table 5.18 make a tentative selection of corrugation profile and sheet thickness as follows: 223-in (68-mm) X f2-in (13-mm) corrugation profile, 0.064-in (1.63 mm) thickness. Properties are
A = 0.775 in2/ft = rff = 0.0646 in2/in (0.137 mm2/mm) > 0.118 in2/ft required (0.250 mm2/mm)
I = 0.0227 in4/ft = ffin>/ft = 0.00189 in4/in (31.0 mm4/mm)
r = VrA = V0.00189/0.0646 = 0.171 in (4.34 mm)
Next, check the buckling stress. To determine whether Eq. (5.39) or (5.40) applies, compare the span (48 in or 1200 mm) with
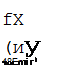 |
|||
Because S < 96.7 in, Eq. (5.39) applies. The buckling stress is
= 39,500 lb/in2 (272 MPa)
Compare this with the yield stress, f = 33,000 lb/in2. Because fcr > fy, buckling does not control. Also, because there are no longitudinal seams, the seam strength check does not apply. Finally, check handling and installation rigidity by calculating the flexibility factor. From Eq. (5.42):
Table 5.21 gives the maximum value of FF for this profile as 4.3 X 10~2 in/lb (0.245 mm/N). Therefore, the design is satisfactory. Select the 233-in (68-mm) X 32-in (13-mm) corrugation profile with a 0.064-in (1.63 mm) sheet thickness.
Structural Design of Pipe by Load Factor Design. Calculations proceed as follows. The thrust in the pipe wall is
![]()
![]() (5.43)
(5.43)
where TL = factored thrust, lb/ft (kN/m)
PL = factored load pressure, lb/ft2 (kPa) S = pipe diameter or span, ft(m)
The required wall area to resist the thrust is
where A = required wall area, in2/ft (mm2/mm) fy = minimum yield stress, lb/in2 (MPa) ф = capacity modification factor
= 1.00 for helical pipe with lock seams or fully welded seams = 0.67 for annular pipe with spot-welded, riveted, or bolted seams (including structural-plate pipe)
After selecting a corrugation profile and sheet thickness, check for possible buckling. If the buckling stress fcr is less than the yield stress, recalculate the area using fcr in lieu offy. The buckling stress is given by Eqs. (5.39) and (5.40). For pipe with longitudinal seams, the required seam strength SS, lb/ft, is
SS = У (5.45)
where ф is as given for Eq. (5.44). Check the flexibility factor by Eq. (5.42) and Table 5.21.
Example: Corrugated Steel Pipe Design via Load Factor Design. For the 48-indiameter (1200-mm) culvert in the preceding example, determine a suitable corrugation and sheet thickness for the culvert.
First, calculate the factored load as follows:
Pl T(PePel + PePll +1)
= 1.3 (1.5 X 771.6 + 1.67 X 200) = 1938.8 lb/ft2 (92.8 kPa)
Then, from Eq. (5.43), the factored thrust in the pipe wall is
= 1938^ у j
= 3877.6 lb/ft (56.6 kN/m)
From Eq. (5.44), the required wall area to resist the thrust is
![]() 1l_
1l_
Ф fy
3877.6
= 1.0 (33,000)
= 0.118 in2/ft (0.250 mm2/mm)
The remaining checks are similar to those for service load design. It can be seen that a satisfactory design is provided with the 233-in (68-mm) X (f-in (13-mm) corrugation profile with a 0.064-in (1.63-mm) sheet thickness.
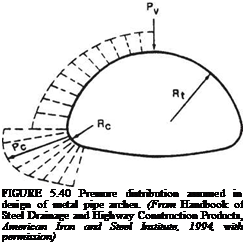
Pipe-Arch Design. The pipe-arch type of steel or aluminum culvert exerts high pressures at the corner radii, as illustrated in Fig. 5.40. For this reason, in addition to the need for designing a pipe to withstand the imposed loads, the soil at the corner radii must
be able to withstand the high bearing pressures applied to it. The anticipated corner pressure for an HS 20 live load can be calculated as follows:
![]()
 |
(^1^LL + PEl) rl
where C1 = y1 when L2 < 72 in L2
C1 = 2 У when L2 > 72 in
L3
Pc = corner pressure, lb/ft2 (kPa)
rl = radius of the pipe-arch crown, in (mm)
rc = corner radius of the pipe arch, in (mm)
L1 = 40 + (h – 12) 1.75 L2 = L1 + 1.37s
L3 = L2 + 72
h = height of cover, in (mm) s = pipe span, in (mm)
In the application of the corner pressure equation, live load impact is not considered. Therefore, the live load pressures given in Table 5.20 should be modified to remove the impact effects. Also, in lieu of the described calculations, C1 can conservatively be assumed to be 1.
Structural Design of Long-Span and Box Culverts. Structural-plate structures that cannot, because of their long span, meet the design requirements for structural-plate pipe structures are defined as long-span structural-plate structures. These structures, which often serve as short-span bridges, are not required to meet buckling or flexibility requirements but must have certain special features (see Art. 5.6.2). The required wall area of the corrugated metal plate is determined by the same method as for other corrugated metal pipe—Eq. (5.38) or Eq. (5.44)—but the span in the equations is replaced by twice the
radius of the top arc. In addition, certain minimum thicknesses that have been found satisfactory through experience are specified by AASHTO for the top-arc plate. Also, the structure must exhibit special features accepted by AASHTO. The design requirements for long-span structures have been based not on an analytical analysis of the soil-structure interaction system, but upon experience with successful installations. There is ongoing research to provide for an analytical and reasonably simple method for the design of these structures.
Corrugated metal box culverts are fabricated from corrugated metal structural plate. The effects of moments on structural-plate box culverts controls over those of thrust. Because of this, box culverts typically require external stiffeners comprised of steel or aluminum structural sections bolted to the exterior of the box culvert. Rib stiffeners are spaced at not less than 2 ft (0.6 m) along the crown and not less than 4.5 ft (1.4 m) along the haunch. Design moments may be calculated from simple tables provided in AASHTO and compared against allowable moments supplied by the manufacturer of the product. Similar to any rigid frame, the moment distribution between the haunch and crown is a function of their relative stiffness. Stiffening one member attracts additional moment, thus shedding moment from the other. In the design of corrugated metal box culverts, the proportioning of the moment is critical to the success of the design. AASHTO provides a proportioning factor along with limiting values to ensure proper moment distribution. Unlike long-span structures, for which the design methodology is based more on experience than analysis, design procedures for metal box culverts have been developed from finite element analysis. The moment capacity includes the consideration of the plastic moment resistance of the structural plate and rib stiffeners.






Leave a reply